ઓર્થોગોનલ બેરેચસઅન્ફ્રાગેન (Orthogonal Range Queries) - મૌખિક પરીક્ષાની તૈયારી
ઓર્થોગોનલ બેરેચસઅન્ફ્રાગેનની સામાન્ય સમજ
ઓર્થોગોનલ બેરેચસઅન્ફ્રાગે એ એક મહત્વપૂર્ણ કમ્પ્યુટેશનલ જ્યોમેટ્રી અને ડેટા સ્ટ્રક્ચર સમસ્યા છે^1. આ સમસ્યામાં આપણને નીચેની બાબતો આપવામાં આવે છે:
- ઇનપુટ: d-dimensional space માં પોઇન્ટ્સનો સમૂહ P
- ક્વેરી: એક axis-parallel (અક્ષોની સમાંતર) રેક્ટેંગલ રેન્જ R
- આઉટપુટ: તે પોઇન્ટ્સ કે જે આપેલ રેન્જ R માં આવે છે
આ પ્રકારની ક્વેરીઓનો ઉપયોગ ડેટાબેઝ એપ્લિકેશનમાં વારંવાર થાય છે, જેમ કે કારના ઉત્પાદન વર્ષ અને છેલ્લી નોંધણીની તારીખના આધારે કારની શોધ કરવી^1.
1-dimensional બેરેચસઅન્ફ્રાગેન માટે ડેટા સ્ટ્રક્ચર
મુખ્ય ડેટા સ્ટ્રક્ચર: બાઇનરી સર્ચ ટ્રી
1-dimensional range queries માટે height-balanced binary search tree (જેમ કે Red-Black Tree) એ શ્રેષ્ઠ પસંદગી છે^1. આ ડેટા સ્ટ્રક્ચર નીચેના complexity characteristics ધરાવે છે:
- નિર્માણ: O(n log n)
- ક્વેરી પ્રોસેસિંગ: O(log n + k), જ્યાં k = પરિણામોની સંખ્યા
- સ્થળ: O(n)
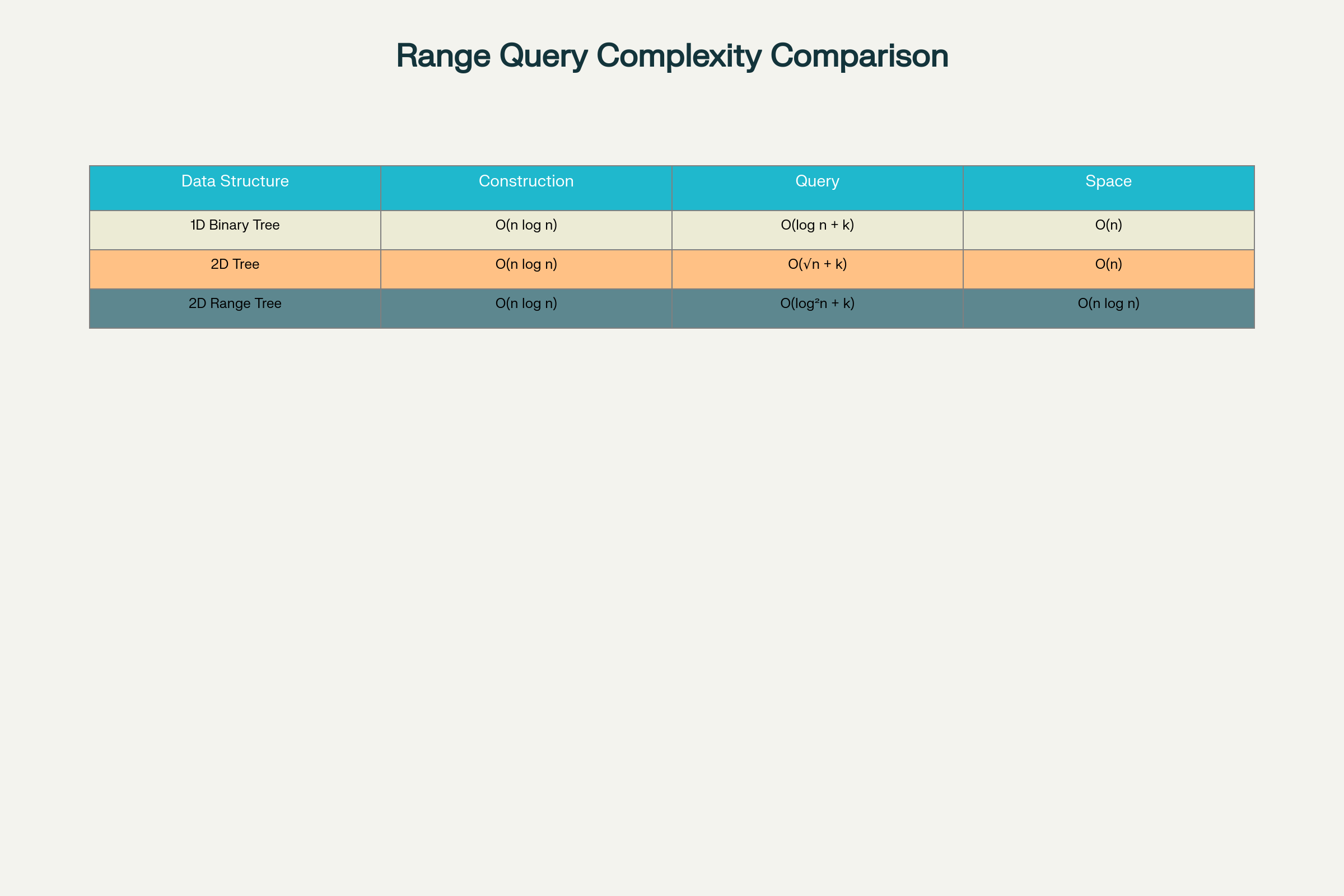
Complexity Comparison of Range Query Data Structures
1D Range Query નું વિગતવાર ઉદાહરણ
ચાલો એક concrete example લઈએ: મધ્યમાં elements {1, 3, 5, 7, 9, 12, 15, 18, 20, 25} છે અને આપણે range ^2 માં આવતા elements શોધવા છે.
Algorithm ના steps:
- પ્રથમ પગલું: Binary search tree માં value 'a' (7) શોધો
- બીજું પગલું: Binary search tree માં value 'b' (18) શોધો
- ત્રીજું પગલું: બંને search paths વચ્ચેના તમામ subtrees traverse કરો
- પરિણામ આપો: range માં આવતા તમામ values
આ ઉદાహરણમાં પરિણામ હશે: {7, 9, 12, 15, 18}
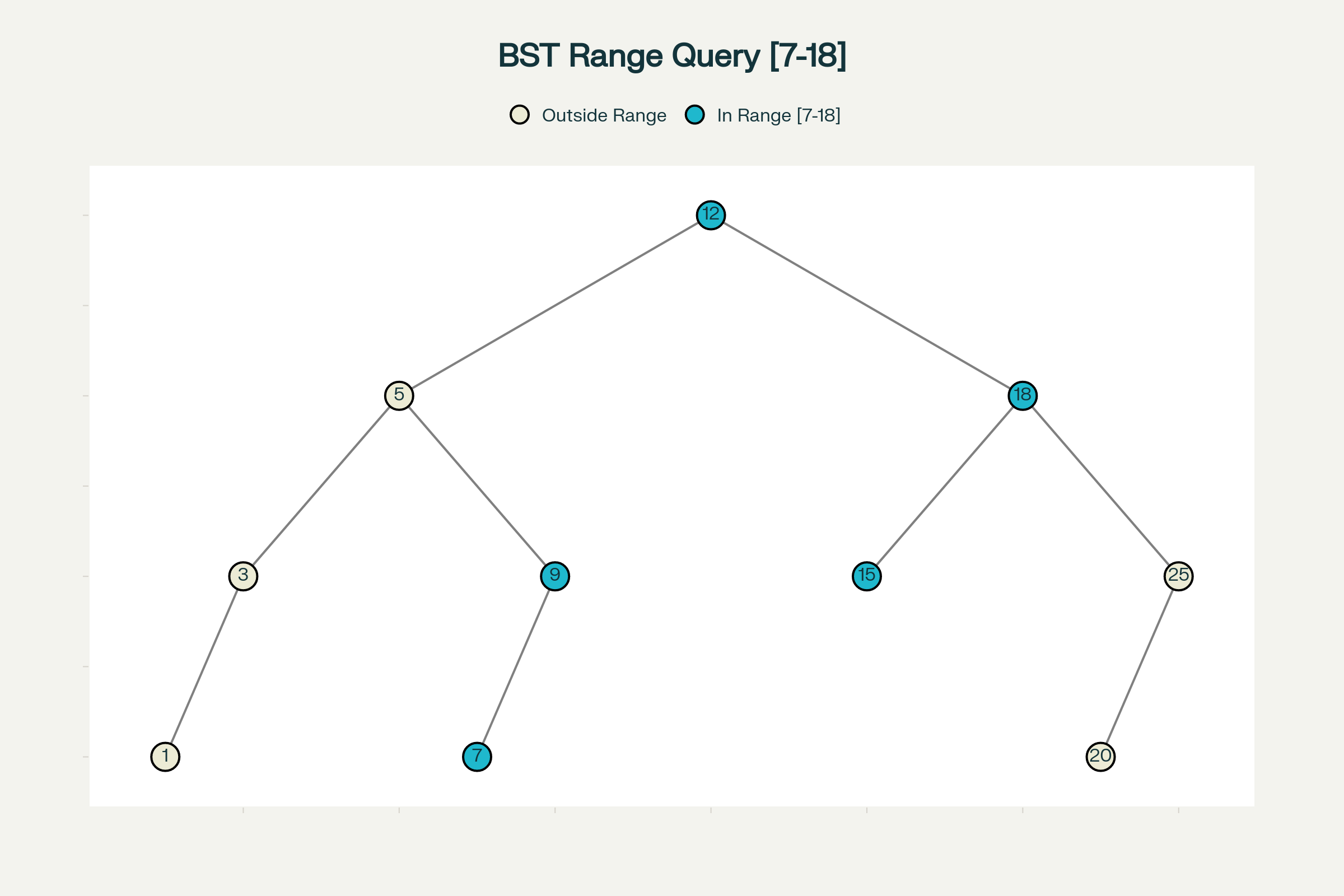
1D Range Query Example: Finding values between 7 and 18 in a Binary Search Tree
Complexity Analysis:
- a અને b શોધવા માટે: O(log n)
- સંપૂર્ણ subtrees traverse કરવા માટે: O(k)
- કુલ complexity: O(log n + k) - આ એક output-sensitive પ્રક્રિયા છે^1
2-dimensional બેરેચસઅન્ફ્રાગેન્સમાં કઠિનાઈઓ
જ્યારે આપણે 1D approach ને 2D પર લાગુ કરવાનો પ્રયાસ કરીએ છીએ, ત્યારે ઘણી મુશ્કેલીઓ ઊભી થાય છે:
પ્રથમ અભિગમ: 2d-Tree (kd-tree)
નિર્માણ પ્રક્રિયા:
- વૈકલ્પિક રીતે vertical અને horizontal splits કરો
- દરેક level પર splitting direction બદલો
- Points ને recursive રીતે વહેંચો^1
મુશ્કેલીઓ:
- Query complexity બહુ ખરાબ છે: O(√n + k)^1
- આ linear time કરતાં વધુ સારું નથી
- Practical applications માટે અપર્યાપ્ત performance
2-dimensional બેરેચસઅન્ફ્રાગેન્સનો કાર્યક્ષમ ઉકેલ: Range Trees
Range Trees નો મુખ્ય વિચાર
2D range query ને બે 1D range queries માં વિભાજિત કરવાનો વિચાર^1:
આર્કિટેક્ચર:
- Primary Structure: x₁-coordinates પર આધારિત binary search tree
- Secondary Structures: દરેક node માં x₂-coordinates પર આધારિત secondary binary search tree
Range Tree નો Algorithm
Construction Phase:
- Points ને x₁-coordinates પ્રમાણે sort કરો
- x₂-coordinates પ્રમાણે પણ sort કરો
- Primary tree બનાવો
- દરેક node માં secondary tree બનાવો^1
Query Processing:
- Primary tree માં [a₁, b₁] range શોધો
- દરેક relevant secondary tree માં [a₂, b₂] range શોધો
- Results combine કરો
Complexity Analysis
Range Trees માટે Runtime Bounds:
| Operation |
Complexity |
| Construction |
O(n log n) |
| Query |
O(log²n + k) |
| Space |
O(n log n) |
Detailed Analysis:
- Primary tree search: O(log n)
- Secondary trees searched: O(log n)
- દરેક secondary tree search: O(log n + kᵤ)
- કુલ query time: O(log²n + k)^1
વધુ સુધારા
Range trees ની query complexity ને O(log²n + k) થી O(log n + k) સુધી સુધારી શકાય છે fractional cascading technique નો ઉપયોગ કરીને^1.
વ્યવહારિક ઉપયોગો
Real-world Applications:
- Computer Graphics: Rectangular clipping operations
- GIS Applications: Spatial data queries
- Database Systems: Multi-dimensional indexing
- CAD Systems: Geometric object selection^1
મહત્વપૂર્ણ બિંદુઓ - પરીક્ષા માટે
યાદ રાખવા જેવા key points:
- 1D case: Binary search tree, O(log n + k) query time
- 2D naive approach: kd-tree, O(√n + k) - inefficient
- 2D optimal solution: Range tree, O(log²n + k)
- Space trade-off: 1D uses O(n), 2D uses O(n log n)
- Output sensitivity: બધા solutions output-sensitive છે
મહત્વપૂર્ણ complexity પરિવર્તનો:
- 1D → 2D: Query time O(log n) → O(log²n)
- 1D → 2D: Space O(n) → O(n log n)
- Construction time બંને માટે O(n log n) સમાન રહે છે
આ સમગ્ર વિષય computational geometry અને advanced data structures નો મહત્વપૂર્ણ ભાગ છે અને પ્રેક્ટિકલ applications માં વ્યાપક રીતે ઉપયોગ થાય છે.
⁂


