પોલિનોમ ઇન્ટરપોલેશન આંકયુગલ (અંકગણિત + ભૌતિક) જ્ઞાનમાં મૂળભૂત સાધન છે. ટૂંકમાં, આપેલ અંતર્પોલેશન બિંદુઓને ચોક્કસ ક્રમના એકમાત્ર પોલિનોમ વડે બાંધી શકાય છે—પરંતુ ક્યારે, કયા સ્વરૂપે અને કેટલી સંખ્યામાં આ પોલિનોમ અનન્ય બને છે, તથા આ પ્રક્રિયાની અંકીય સ્થિરતા (condition) કેવી રીતે આંકી શકાય—આ પ્રશ્નો પર સ્પષ્ટ સમજણી વિના કોઈ પણ મૌખિક પરીક્ષા પાર પાડવી મુશ્કેલ બની શકે. નીચેના વિભાગો આ તમામ મુદ્દાઓને વિગતવાર, אך સરળ ગુજરાતી ભાષામાં, દસ મિનિટ ની પ્રસ્તુતિ માટે લાયક ક્રમ અને ઉદાહરણો સહિત समઝાવે છે.
(x_i, y_i) માટે $i=0,1,\dots ,n$ સુધીના સુવિકલ સ્થિરબિંદુઓ, જ્યાં $x_i$ સંપૂર્ણ એકબીજાથી અલગ (સપષ્ટ) હોઇ અને $y_i$ સંખ્યાત્મક મૂલ્યો છે.પ્રથમ મહત્વનું પ્રશ્ન એ છે કે કેટલા શરતો હેઠાને એવો પોલિનોમ એકજ મળે?
ડીજિટલ ગણા-ગણિત માં એકળઇ પોલિનોમ BC પણ છ કે તે હજુ કેવી રીતે વર્ણવવામાં આવે—પ્રત્યેક આકાર વિશિષ્ટ ગુણ અને ા સંખ્યિતિ હાંસલ કરાવે છે.
$p_n(x) = c_0 + c_1 x + c_2 x^2 + \dots + c_n x^n$
લેખીત સરળ છે પણ ઉચ્ચ ડિગ્રી પર અંકીય અસ્થિર થવાની (પાવર અધિક છ તો $x^n$ વિશાળ/નાનું ભી વધારે) શક્યતા વધે.
$p_n(x)=\sum_{i=0}^{n} y_i,\ell_i(x)$
અહીં $\ell_i(x)$ લાગ્રાંજ આધાર પોલિનોમ ,$\ell_i(x_j)=\delta_{ij}$.
$p_n(x)=a_0 + a_1(x-x_0)+a_2(x-x_0)(x-x_1)+\dots$
$$
p_n(x)=\frac{\displaystyle\sum_{i=0}^{n}\frac{w_i,y_i}{x-x_i}}{\displaystyle\sum_{i=0}^{n}\frac{w_i}{x-x_i}},
\quad w_i=\frac1{\prod_{j\ne i}(x_i-x_j)}
$$
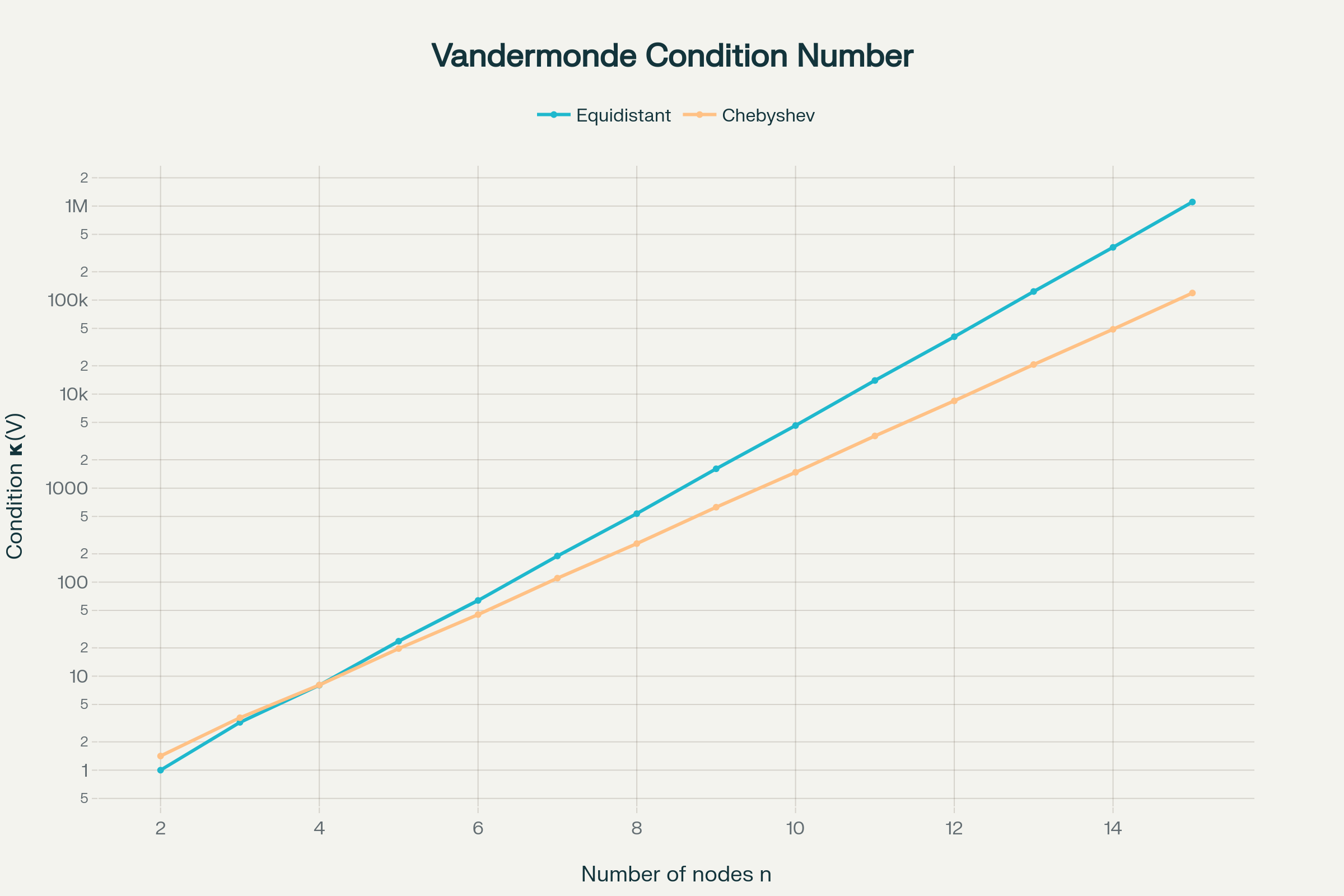
કન્ડિશન સંકલ્પ અંકીય vis-વૈજ્ઞાનિક અર્થે એવું પૂછે છે કે:
“ઇનપુટ ડેટાની સૂબક્ષ ભૂલ $\delta y$ અથવા $\delta x$ પોલિનોમ $p_n$ નાં ઉત્પન્ન મૂલ્યો-પર શા ટ ટાડા ઉલટ પડકાર રૂપે વિસ્તરે છે?”
આ સંવેદનશીલતા પર આધારિત સંખ્યાતંત્ર વધારાની ભૂલ ઉપજાવી શકે કે ન — તે માપવા **કન્ડિશન નંબર $\kappa$** ઉપયોગ થાય.

Kondition des Vandermonde-Systems für Equidistante vs. Chebyshev-Knoten
| વર્ણનપદ્ધતિ | મૂળભૂત લાભ | સંભવિત અવગુણ | શ્રેષ્ઠ ઉપયોગ પ્રસંગ |
|---|---|---|---|
| Power Basis | ગણિતમાં સરળ ભાગ વાણી | ઊંચી ડિગ્રી પર અંકીય અસ્થિર | લઘુ ડિગ્રી અને સૈદ્ધાંતિક અભ્યાસ |
| Lagrange | બંધબેસતું સૂત્ર, ચોક્કસ જરુર વાળા ફોર્મ | દરેક નવા બિંદુ માટે ફેર સુત્ર ફરી કલક્યૂ. | સાદી શ્રેણી ડેટા, સાધારણ ઍન્ગિનિયલૂ પ્રશ્ન |
| Newton | ઇનક્રિમેન્ટલ અપડેટ સાધ્ય | ક્રમાંકન અનુક્રમ પર નિર્ભર | કૌસલ/કદમ ઉચ્ચ ડિગ્રી રાહત |
| Barycentric | શ્રેષ્ઠ અંકીય સ્થિરતા, ઝડપ | વજન $w_i$ પૂર્વે હિસાબ જરૂરી | બહુવિધ evaluations, ગ્રાફ ડ્રોઇંગ, કન્ડિશન વિશ્લેષણ |
આ બધા બિંદુઓ ન મુખ્ય સૂત્ર, વ્યાખ્યા અને ઉદાહરણ તમારી દસ મિનિટ ની મૌખિક પરીક્ષા માટે પર્યાપ્ત ધિર આધાર પાદ અરૂપ એટલું વિસ્તાર આ નિબંધ રમાં સમાવેલું છે. વાંચન પછી સમય લઈ ખુદ સાથે પ્રશ્નો ઉઠાવો—જેમ ક “કઈ સ્થિતિ માં ન્યુટન રુપ શ્રેષ્ઠ છે?”—અને આ પોઈન્ટ આપથી જ સમજશો તો પરીક્ષક ની પ્રશ્નોત્તરી સુમેળ સાથે ઉત્તર આપી શકશો.