સાંખ્યિક એકીકરણ (Numerical Integration) - મૌખિક પરીક્ષા તૈયારી

તમારી ગણિત ૩ ની મૌખિક પરીક્ષા માટે સાંખ્યિક એકીકરણની વિગતવાર માહિતી અહીં પ્રસ્તુત છે. આ મહત્વપૂર્ણ વિષયને સમજવા માટે અમે પાંચ મુખ્ય પ્રશ્નોના ઉત્તરો આપીશું.

૧. સાંખ્યિક એકીકરણની જરૂરિયાત શા માટે પડે છે?

સાંખ્યિક એકીકરણની જરૂરિયાત મુખ્યત્વે ત્રણ કારણોસર પડે છે^1:

મુખ્ય કારણો:

પ્રથમ કારણ - અજ્ઞાત આદિમ વિધર્મી (Unknown Antiderivatives)

• કેટલાક વિધર્મો માટે આદિમ વિધર્મી શોધવાનું અશક્ય હોય છે
• ઉદાહરણ: ∫₀¹ (1/√2π)e^(-x²/2) dx જેવા સામાન્ય વિતરણના સમીકરણો^1
• આવા વિધર્મોને elementary functions થી વ્યક્ત કરી શકાતું નથી

બીજું કારણ - માત્ર સંખ્યાત્મક મૂલ્યો ઉપલબ્ધ

• કોમ્પ્યુટર ગ્રાફિક્સમાં લાઇટ મોડેલિંગ જેવા કિસ્સાઓમાં વિધર્મી ફક્ત ચોક્કસ સ્થળોએ જ મેળવી શકાય છે^1
• પ્રયોગશાળાના માપણ અથવા સેન્સર ડેટા દ્વારા મળેલા બિંદુઓ

ત્રીજું કારણ - કાર્યક્ષમતા (Efficiency)

• કેટલાક વખતે આદિમ વિધર્મી અસ્તિત્વમાં હોય પણ તેની ગણતરી ખૂબ જટિલ અથવા ધીમી હોય છે

૨. બહુપદી અનુમાનન દ્વારા સાંખ્યિક એકીકરણ

સૈદ્ધાંતિક અભિગમ:

પ્રાથમિક પગલાં^1:

1. સ્ટુત્ઝસ્ટેલેન (Support Points) પસંદ કરવા: a = x₀ < x₁ < x₂ < ... < xₙ = b
2. વિધર્મીના મૂલ્યો મેળવવા: y₀ = f(x₀), y₁ = f(x₁), ..., yₙ = f(xₙ)
3. અનુમાનન બહુપદી બનાવવું: p(x) જે આ બિંદુઓમાંથી પસાર થાય
4. એકીકરણ કરવું: ∫ₐᵇ f(x)dx ≈ ∫ₐᵇ p(x)dx

લાગ્રાંજ બહુપદી સાથે વ્યાખ્યા:

સૂત્ર: ∫ₐᵇ f(x)dx ≈ ∑ₖ₌₀ⁿ yₖ gₖ

જ્યાં gₖ = ∫ₐᵇ Lₖ(x)dx એ વેઇટિંગ વેલ્યુ છે^1.

૩. અનુમાનન બહુપદીના એકીકરણની સમસ્યાઓ

મુખ્ય સમસ્યાઓ:

ખરાબ કન્ડિશનિંગ (Poor Conditioning)^1:

• n > 10 સ્ટુત્ઝસ્ટેલેન માટે સમસ્યા ભયંકર બને છે
• સમાન અંતરાલે મુકવામાં આવેલા બિંદુઓ માટે વધુ ખરાબ પરિણામો
• નાના ફેરફારો મોટા ભૂલો તરફ દોરી જાય છે

રુંગે ઇફેક્ટ (Runge Effect)^2:

• ઉચ્ચ ડિગ્રીના બહુપદીઓ અનાવશ્યક વધઘટ બતાવે છે
• ખાસ કરીને અંતરાલની કિનારીઓ પર અસ્થિરતા

વ્યાવહારિક મુશ્કેલીઓ:

• ઘણા બધા સ્ટુત્ઝસ્ટેલેનની જરૂરિયાત પણ સંખ્યાત્મક ગણતરી મુશ્કેલ બનાવે છે^1

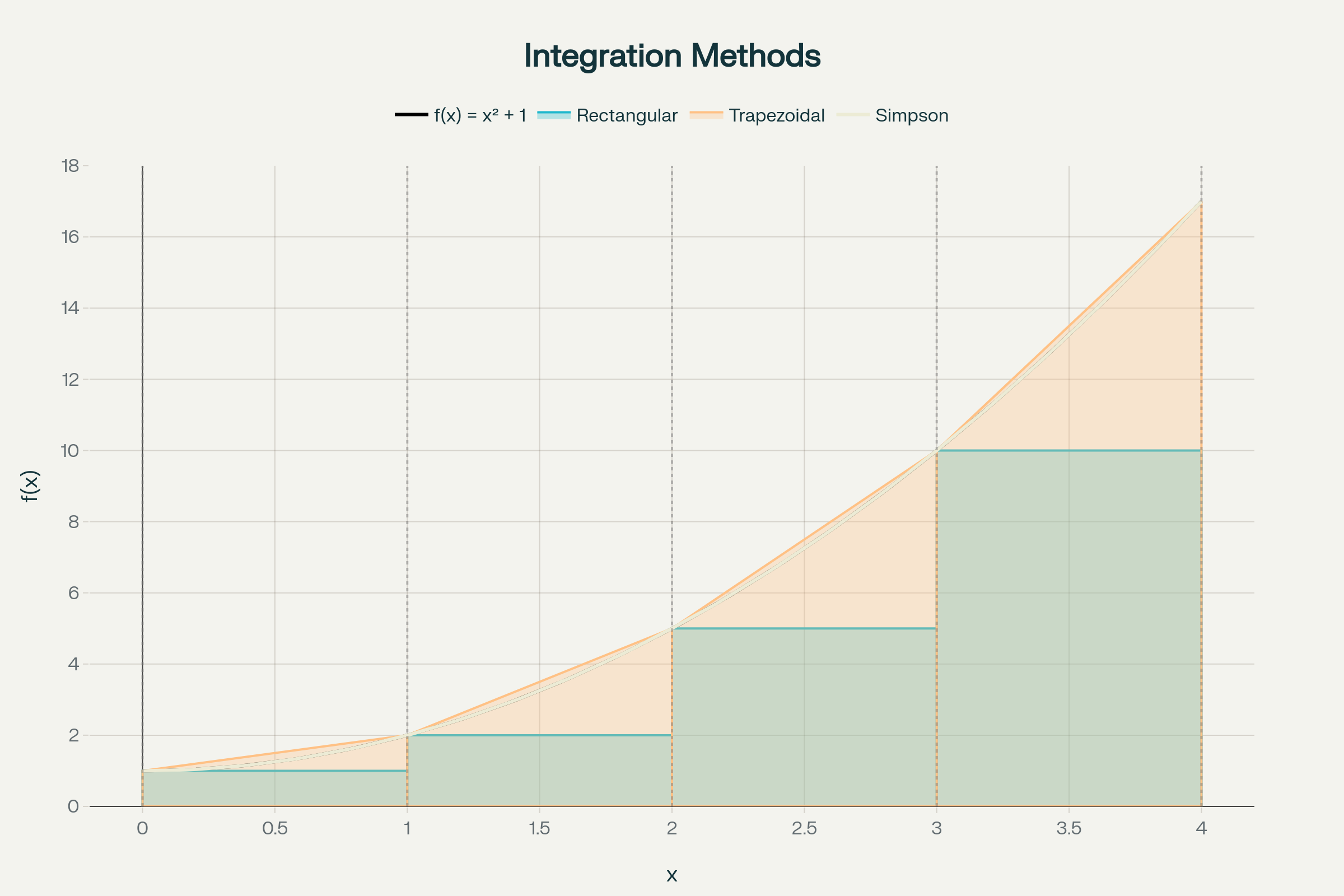
Comparison of Numerical Integration Methods: Rectangular, Trapezoidal, and Simpson's Rule

૪. વ્યવહારિક પદ્ધતિ - સિમ્પસન નિયમ (Simpson's Rule)

સિમ્પસન નિયમ (કેપ્લર નિયમ):

મૂળભૂત સૂત્ર^1:
જો n સમ હોય તો:

∫ₐᵇ f(x)dx ≈ (h/3)[y₀ + 4y₁ + 2y₂ + 4y₃ + 2y₄ + ... + 4yₙ₋₁ + yₙ]

જ્યાં h = (b-a)/n અને yᵢ = f(xᵢ)

વિગતવાર ઉદાહરણ:

વિધર્મી: f(x) = e^(-x²/2)/√(2π) (ગૌસીયન વિધર્મી)
અંતરાલ: [-2, 2]
સચોટ મૂલ્ય: 0.95449974

વિવિધ n માટે પરિણામો:

• n=4: સિમ્પસન પરિણામ = 0.947211, ભૂલ = 0.007289
• n=8: સિમ્પસન પરિણામ = 0.954402, ભૂલ = 0.000098
• n=16: સિમ્પસન પરિણામ = 0.954495, ભૂલ = 0.000005
• n=32: સિમ્પસન પરિણામ = 0.954499, ભૂલ = 0.0000003

અન્ય વ્યાવહારિક પદ્ધતિઓ:

1. ટ્રેપેઝોઇડલ નિયમ (Trapezoidal Rule)^1:

∫ₐᵇ f(x)dx ≈ (h/2)[y₀ + 2y₁ + 2y₂ + ... + 2yₙ₋₁ + yₙ]

2. આયતાકાર નિયમ (Rectangular Rule)^1:
મધ્યબિંદુ પદ્ધતિ: ∫ₐᵇ f(x)dx ≈ h∑f(xᵢ₊₁/₂)

૫. ભૂલ નિયંત્રણ અને અચોક્કસતાનું સંચાલન

ભૂલના ક્રમ (Error Orders):

સૈદ્ધાંતિક ભૂલ અંદાજ^1:

• આયતાકાર નિયમ: ભૂલ ∝ h³/3 × max|f''(x)|
• ટ્રેપેઝોઇડલ નિયમ: ભૂલ ∝ h³/12 × max|f''(x)|
• સિમ્પસન નિયમ: ભૂલ ∝ h⁵/90 × max|f⁽⁴⁾(x)|

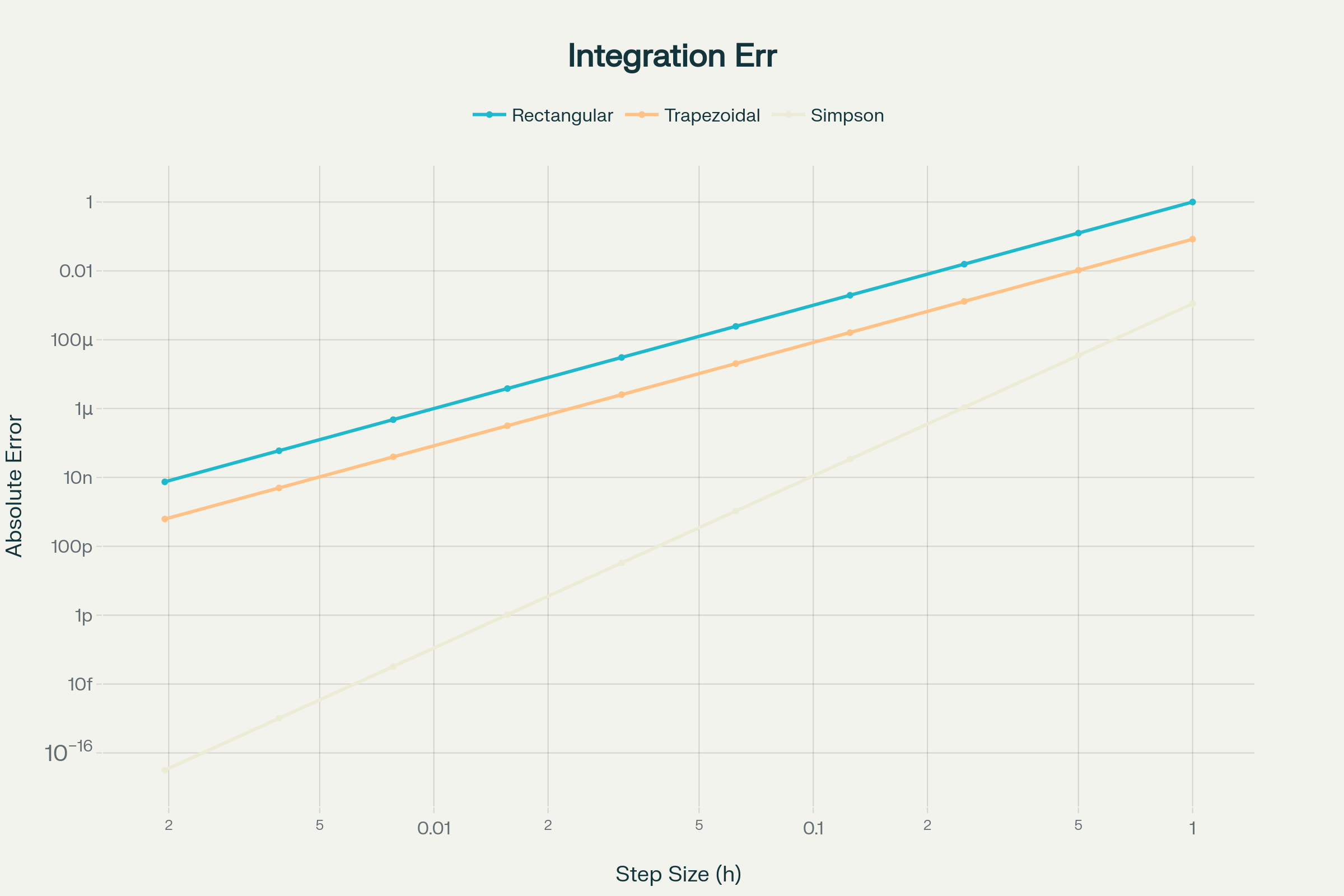
Error Analysis: Convergence Rates of Numerical Integration Methods

ભૂલ નિયંત્રણની પદ્ધતિઓ:

1. અનુકૂલનીય પદ્ધતિ (Adaptive Methods):

• પ્રારંભમાં મોટા h સાથે ગણતરી
• જરૂરિયાત મુજબ h ઘટાડીને બિનચોકસાઈ ઘટાડવી
• નિર્ધારિત સહનશીલતા પહોંચે ત્યાં સુધી પુનરાવૃત્તિ

2. રિચાર્ડસન એક્સ્ટ્રાપોલેશન:

• બે વિવિધ h મૂલ્યો સાથે ગણતરી
• ભૂલનો અંદાજ: Error ≈ |I(h) - I(h/2)|
• સુધારેલ પરિણામ મેળવવો

3. પ્રાયોગિક ભૂલ જાણકારી:
અમારા ઉદાહરણમાં જ્યારે h અડધું થાય છે:

• સિમ્પસન ભૂલ લગભગ 16-32 ગણું ઘટે છે (સૈદ્ધાંતિક રીતે 32 ગણું અપેક્ષિત છે)
• ટ્રેપેઝોઇડલ ભૂલ લગભગ 4 ગણું ઘટે છે

વ્યાવહારિક સલાહ:

પદ્ધતિ પસંદગી:

• સરળ વિધર્મો માટે: ટ્રેપેઝોઇડલ નિયમ પૂરતો
• ઉચ્ચ ચોકસાઈ જરૂરી: સિમ્પસન નિયમ
• અતિ જટિલ વિધર્મો માટે: અનુકૂલનીય પદ્ધતિઓ

ભૂલ મર્યાદા સેટિંગ:

• જરૂરિયાત મુજબ સહનશીલતા નક્કી કરવી (ઉદા: 10⁻⁶)
• પુનરાવૃત્તિક સુધારણા જ્યાં સુધી મર્યાદામાં ન આવે
• કોમ્પ્યુટેશનલ કિંમત અને ચોકસાઈ વચ્ચે સંતુલન

આ સંપૂર્ણ માહિતી તમારી 10 મિનિટની મૌખિક પ્રસ્તુતિ માટે પૂરતી છે. મુખ્ય મુદ્દાઓ યાદ રાખો અને ઉદાહરણો સાથે સમજાવવાની તૈયારી કરો.