આ વિષય મૌખિક પરીક્ષાની તૈયારી માટે ડિફરન્શિયલ એક્વેશન્સના ન્યુમેરિકલ ઉકેલ અને યુલર પદ્ધતિની વિગતવાર સમજૂતી પ્રદાન કરે છે^1। ન્યુમેરિકલ પદ્ધતિઓ ગણિતના તે ક્ષેત્રમાં મહત્વપૂર્ણ છે જ્યાં સીમાબદ્ધ ગણતરીઓ દ્વારા અંદાજિત ઉકેલ મેળવવા પડે છે^3।
અમુક પ્રકારના ડિફરન્શિયલ એક્વેશન્સ માટે સિમ્બોલિક ઉકેલ શોધી શકાય છે, પરંતુ ઘણા વ્યવહારિક એપ્લિકેશન્સમાં આવા એક્વેશન્સનો સામનો કરવો પડે છે જેમનો બંધ સ્વરૂપમાં (closed form) ઉકેલ શક્ય નથી^1। મુખ્ય કારણો નીચે મુજબ છે:
જટિલ વિક્ષેપક ફંક્શન્સ: જ્યારે ડિફરન્શિયલ એક્વેશનમાં આવતા વિક્ષેપક ફંક્શન (störfunktion) સિમ્બોલિક સ્વરૂપમાં ઉપલબ્ધ ન હોય, પરંતુ માત્ર ચોક્કસ બિંદુઓ પર જ તેની ગણતરી અથવા માપણી કરી શકાય^1।
પ્રાયોગિક એપ્લિકેશન્સ: કમ્પ્યુટર ગ્રાફિક્સમાં પ્રવાહી પદાર્થોનું મોડેલિંગ, જ્યાં દરેક કણનું વર્તન ડિફરન્શિયલ એક્વેશન દ્વારા વર્ણવવામાં આવે છે^1। આવા કિસ્સાઓમાં દરેક કણ પર લાગતું બળ (F(t)) અન્य કણોની સ્થિતિ અને વેગના આધારે ન્યુમેરિકલી જ ગણવામાં આવે છે।

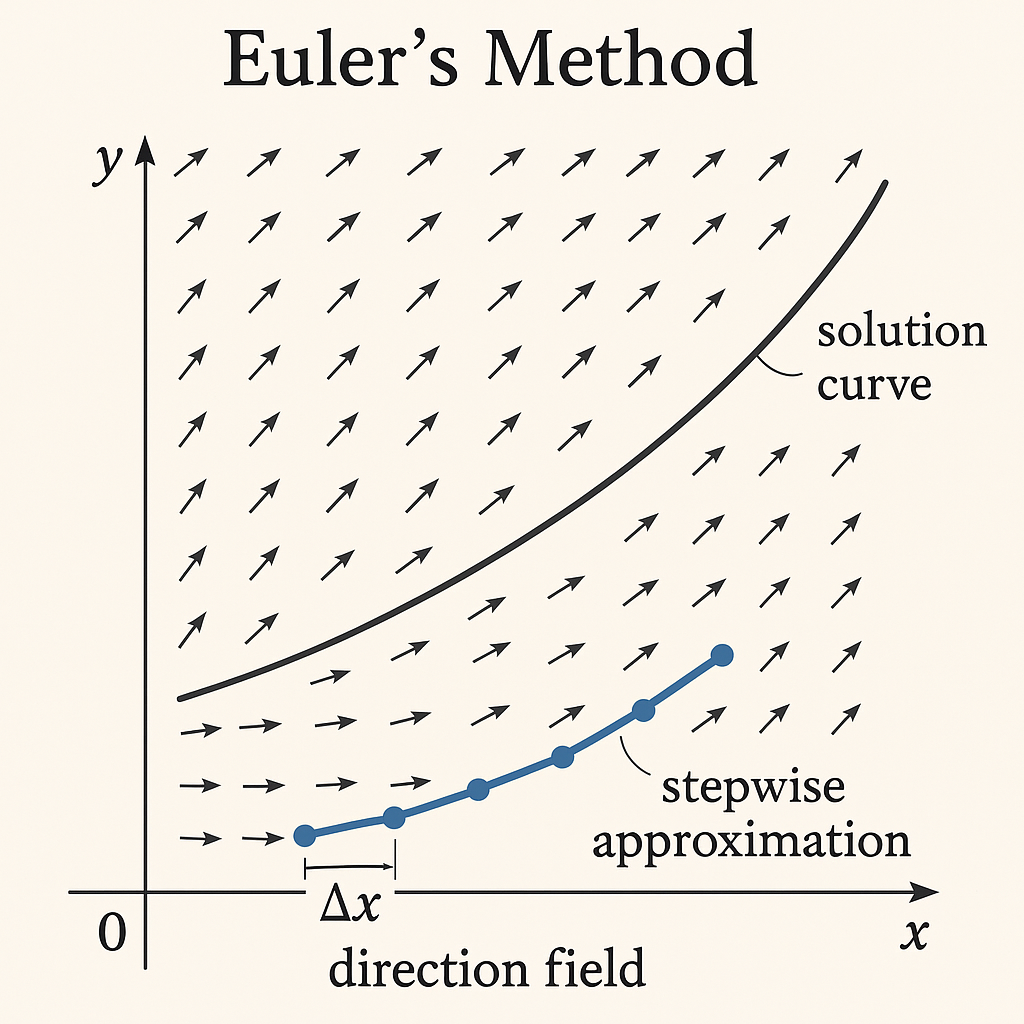
યુલર પદ્ધતિની વિભાવના દર્શાવતું આકૃતિ
કમ્પ્યુટર ગેમ્સ અને સિમ્યુલેશન: અગ્નિ, ધુમાડો અને પાણીના તરંગોનું વાસ્તવિક દર્શન ઘણીવાર ડિફરન્શિયલ એક્વેશન્સના સિસ્ટમ દ્વારા મોડેલ કરવામાં આવે છે।
ઇન્જિનિયરિંગ એપ્લિકેશન્સ: મિકેનિકલ સિસ્ટમ્સ, ઇલેક્ટ્રિકલ સર્કિટ્સ, અને કંટ્રોલ સિસ્ટમ્સમાં ન્યુમેરિકલ ઉકેલ અનિવાર્ય બને છે^1।
ન્યુમેરિકલ પદ્ધતિ માટે નીચેના ઇનપુટ્સની જરૂર પડે છે^1:
ડિફરન્શિયલ એક્વેશન: પ્રથમ ક્રમનું એક્વેશન y'(x) = f(x, y(x)) સ્વરૂપમાં
પ્રારંભિક શરત: y(x₀) = y₀
ડોમેન: અંતરાલ [x₀, x₀ + L], જ્યાં L > 0
આઉટપુટ તરીકે અજ્ઞાત ફંક્શન y(x)ની અંદાજિત વક્રતા મળે છે જે આપેલા અંતરાલ પર ગણવામાં આવે છે^1। આ વક્રતા પ્રારંભિક બિંદુ (x₀, y₀) માંથી પસાર થાય છે અને આપેલા ડિફરન્શિયલ એક્વેશનને સંતોષે છે।
યુલર પદ્ધતિનો મૂળ વિચાર રિક્તંગફેલ્ડ (direction field) પર આધારિત છે^1। દરેક બિંદુ (x₀, y₀) માટે, ડિફરન્શિયલ એક્વેશન y'(x) = f(x, y(x)) એ બિંદુએ સ્પર્શક રેખાનો ઢોળાવ આપે છે।
રિક્તંગવેક્ટર: RF(x₀, y₀) = (1, f(x₀, y₀))
આ વેક્ટર દર્શાવે છે કે જો ઉકેલ વક્ર આ બિંદુમાંથી પસાર થાય તો તેની દિશા શું હશે^1।
પગલાની વિભાજન: અંતરાલને n ભાગમાં વહેંચીને સમાન પગલા-કદ h = L/n લેવામાં આવે છે^1।
પુનરાવર્તક સૂત્ર:
સામાન્ય સૂત્ર:
(xₙ₊₁, yₙ₊₁) = (xₙ, yₙ) + h·(1, f(xₙ, yₙ))
યુલર પદ્ધતિ પ્રથમ ક્રમની પદ્ધતિ છે, એટલે કે વેર્ફાહરેન્સફેહલર (procedural error) F_Euler ∝ h છે^1। પગલા-કદ જેટલો નાનો હશે, ત્યાર ભૂલ તેટલી ઓછી હશે।
સિસ્ટમ:
પ્રારંભિક શરતો: x(0) = 1, y(0) = 0
પગલા-કદ: h = 0.1
દરેક પગલે બન્ને ફંક્શન્સ સાથે સાથે અપડેટ કરવામાં આવે છે^4:
પ્રથમ પગલું (t = 0):
બીજું પગલું (t = 0.1):
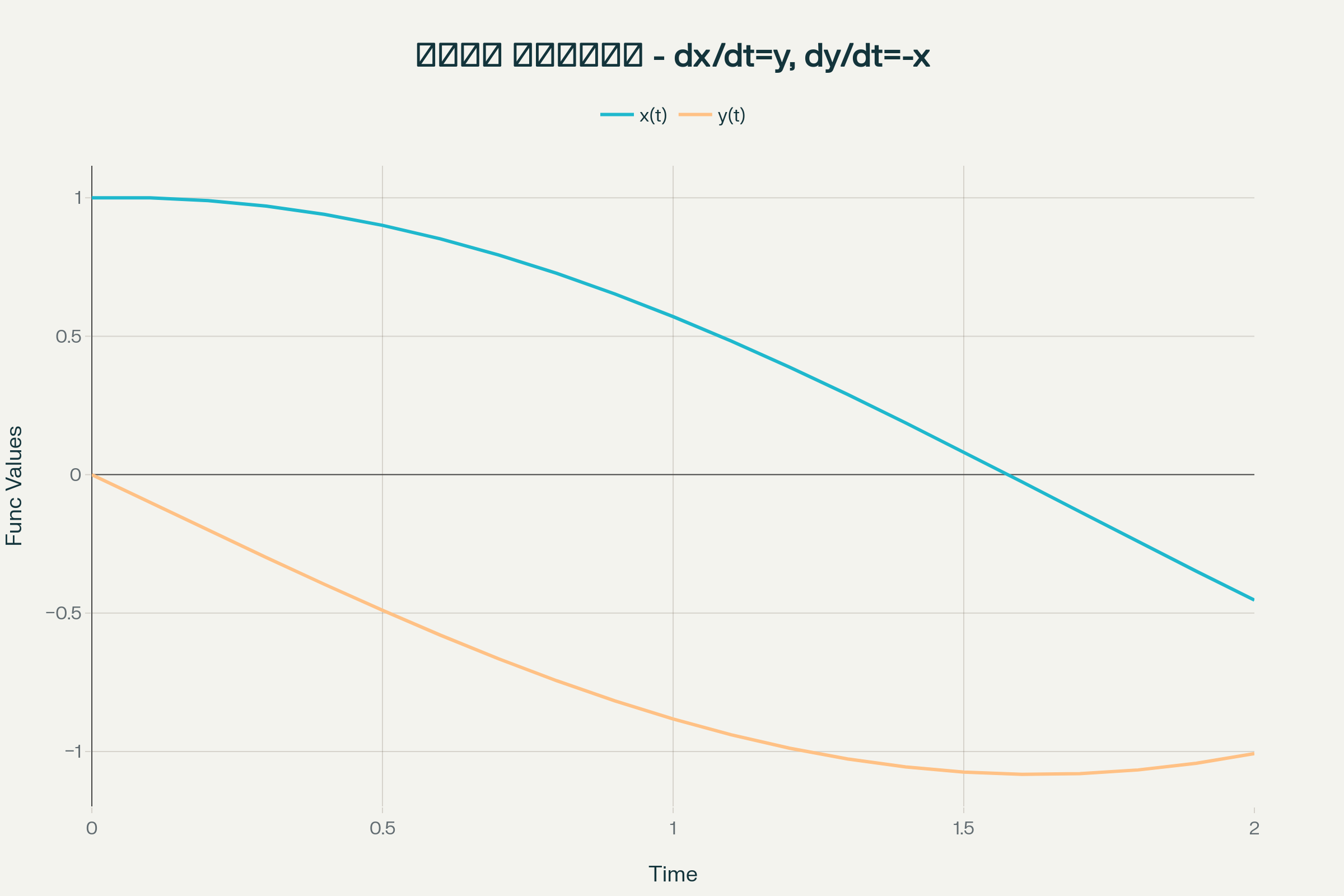
યુલર પદ્ધતિનો ઉપયોગ કરીને સિસ્ટમ ઓફ ડિફરન્શિયલ એક્વેશન્સનો ગ્રાફિકલ પ્રતિનિધિત્વ
જ્યારે n વેરિયેબલ્સ હોય: x₁, x₂, ..., xₙ
સિસ્ટમ:
યુલર અપડેટ:
પાંચ જોડાયેલા માસેસનું સિસ્ટમ^4:
યુલર પદ્ધતિમાં સુધારા માટે પ્રેડિક્ટર-કોરેક્ટર પદ્ધતિ (Heun's method) નો ઉપયોગ કરી શકાય છે^1:
આ પદ્ધતિ બીજા ક્રમની છે અને વધુ સચોટ પરિણામો આપે છે^1।
યુલર પદ્ધતિ ડિફરન્શિયલ એક્વેશન્સના ન્યુમેરિકલ ઉકેલ માટે સૌથી સરળ અને મૂળભૂત પદ્ધતિ છે^1। તે એકલ એક્વેશન તેમજ સિસ્ટમ ઓફ એક્વેશન્સ બંનેમાં લાગુ કરી શકાય છે. જોકે તેની ચોકસાઈ મર્યાદિત છે, પરંતુ તેની સરળતા અને સમજવામાં આવતી સુવિધાને કારણે તે ન્યુમેરિકલ ગણિતમાં પાયાનું કામ કરે છે^1।