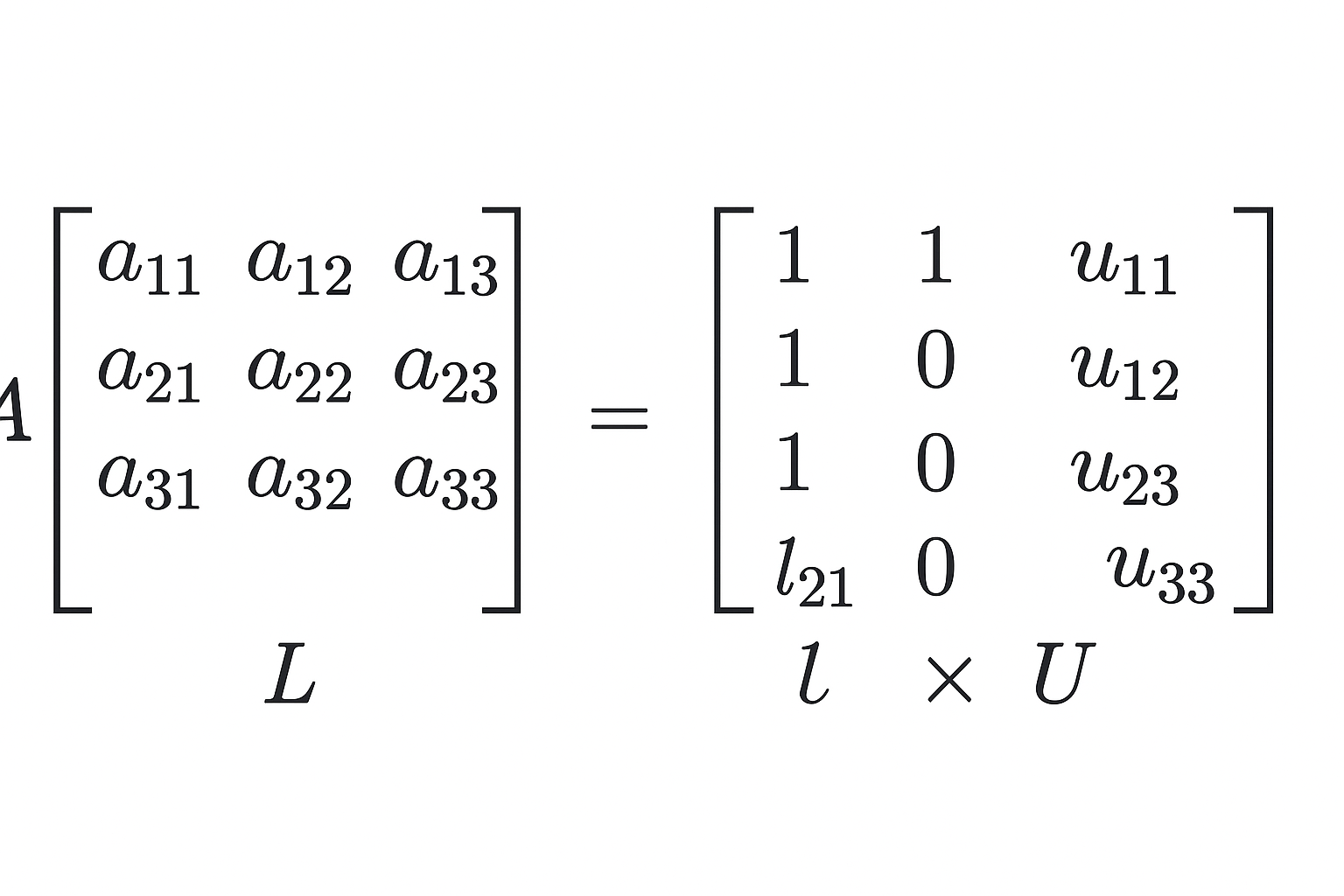
રેખીય સમીકરણ પદ્ધતિઓનો ઉકેલ લાવવો એ ગણિત અને કોમ્પ્યુટર સાયન્સમાં મૂળભૂત કાર્ય છે. LU-વિભાજન (LU-Zerlegung) એ આ કાર્ય માટે એક અત્યંત મહત્વપૂર્ણ અને કાર્યક્ષમ પદ્ધતિ છે જે ગૌસીય નિરાકરણ પદ્ધતિનો વિસ્તાર છે.
LU-વિભાજન એ એક ચોરસ મેટ્રિક્સ A (વાસ્તવિક સંખ્યાઓની અંદરાજો સાથે) ને બે ત્રિકોણાકાર મેટ્રિક્સના ગુણાકાર તરીકે રજૂ કરવાની પદ્ધતિ છે^1:
A = L × U
જ્યાં:
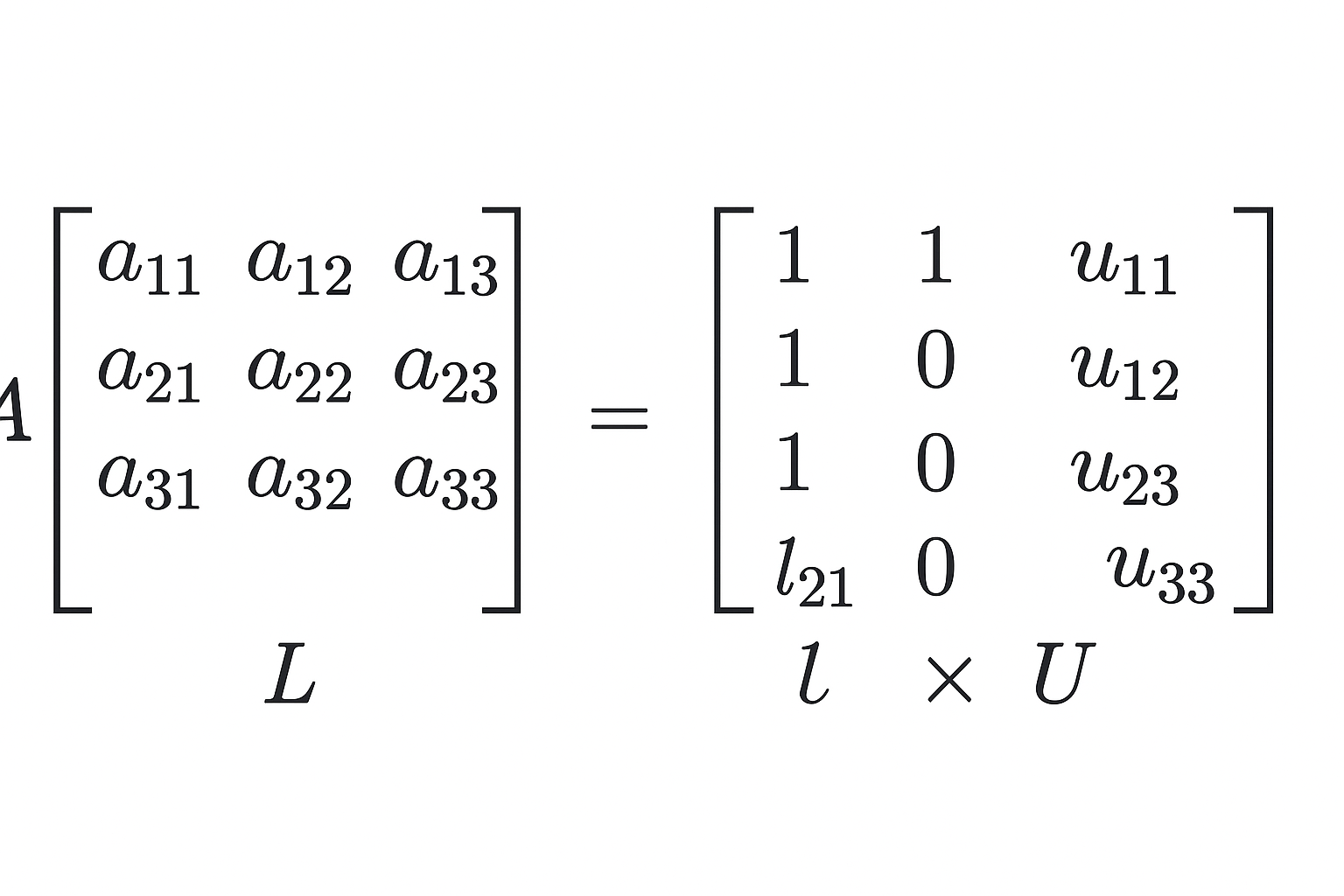
LU Decomposition Matrix Structure Visualization
સામાન્ય રીતે, સંપૂર્ણ વિભાજન આ સ્વરૂપમાં લખવામાં આવે છે:
A = L × U × P
જ્યાં P એ ક્રમચય મેટ્રિક્સ (Permutationsmatrix) છે^1.
A·x = b સ્વરૂપની રેખીય સમીકરણ પદ્ધતિનો ઉકેલ LU-વિભાજનનો ઉપયોગ કરીને બે પગલાંમાં લાવી શકાય છે^1:

LU Decomposition Process Flow for Solving Linear Systems
પ્રથમ L·y = b ને y માટે ઉકેલો:
પછી U·x = y ને x માટે ઉકેલો:
LU-વિભાજનના મુખ્ય લાભો નીચે મુજબ છે^1:
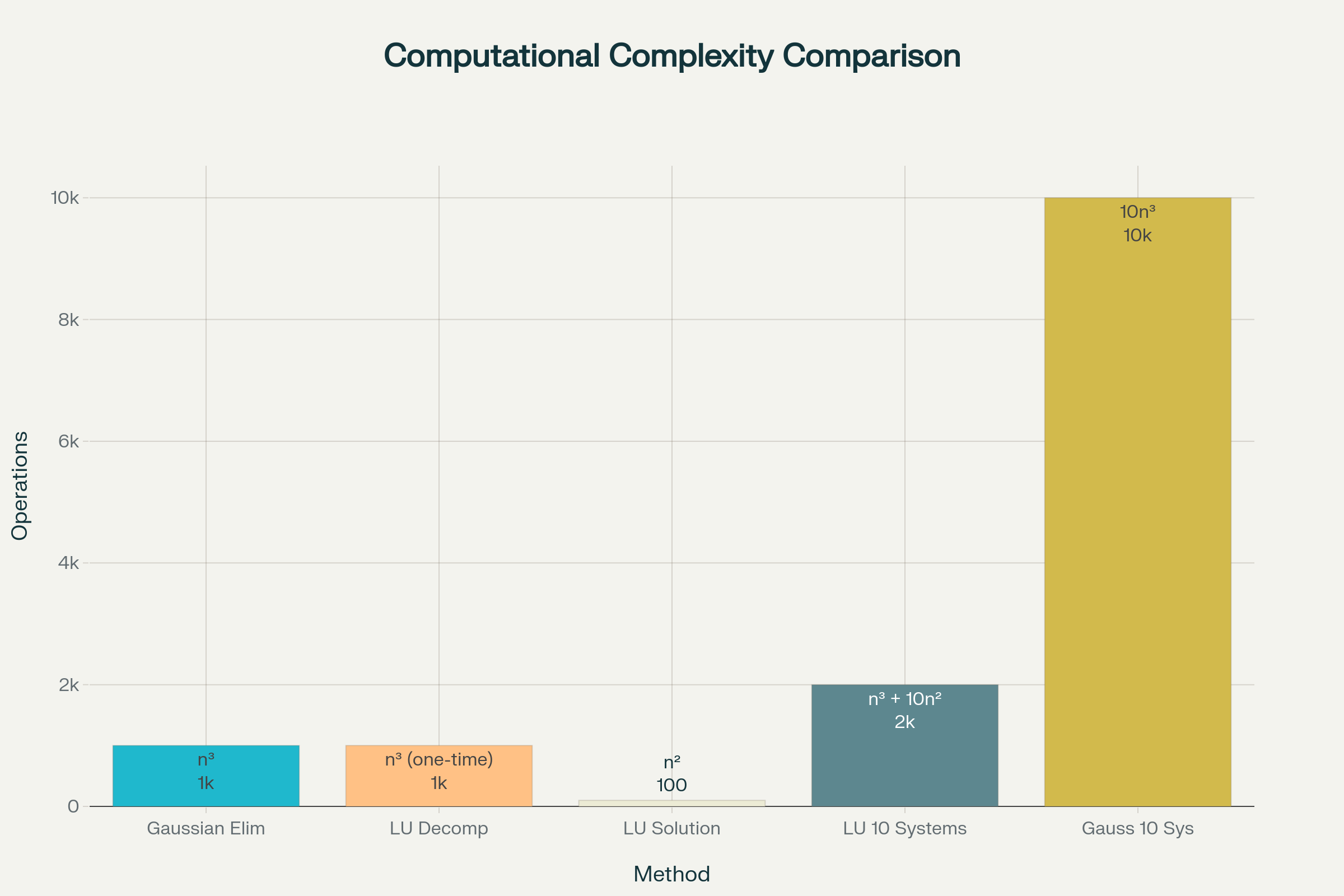
Computational Complexity Comparison: LU Decomposition vs Gaussian Elimination
જ્યારે એક જ સહગુણક મેટ્રિક્સ A સાથે વિવિધ જમણી બાજુઓ b₁, b₂, b₃... માટે ઉકેલ લાવવાનો હોય, ત્યારે:
મેટ્રિક્સનું રૂપાંતરણ અને સિસ્ટમના ઉકેલને અલગ કરી શકાય છે, જેનાથી વધુ લવચીકતા મળે છે.
બહુવિધ સમીકરણ પદ્ધતિઓ માટે નોંધપાત્ર ગણતરીનો સમય બચાવી શકાય છે.
સામાન્ય રીતે LU-વિભાજનમાં વધારાનું ક્રમચય મેટ્રિક્સ P મળે છે, કારણ કે^1:
રેખીય સમીકરણ પદ્ધતિ A·x = b ના અંદાજી ઉકેલ x̃ ની ગુણવત્તાનું મૂલ્યાંકન કરવામાં અનેક મુશ્કેલીઓ ઊભી થાય છે^3:
મેટ્રિક્સની સ્થિતિ સંખ્યા κ(A) = ||A|| · ||A⁻¹|| ઉકેલની ગુણવત્તાને મોટા પ્રમાણમાં પ્રભાવિત કરે છે:
વર્તમાન માપદંડો હંમેશા ઉકેલની ખરી ગુણવત્તાને પ્રતિબિંબિત કરતા નથી, ખાસ કરીને:
LU-વિભાજન એ રેખીય સમીકરણ પદ્ધતિઓ માટે અત્યંત શક્તિશાળી અને કાર્યક્ષમ સાધન છે. તેના મુખ્ય લાભો કાર્યક્ષમતા, લવચીકતા અને પુનઃઉપયોગની ક્ષમતામાં રહેલા છે. જો કે, સંખ્યાત્મક સ્થિરતા માટે ક્રમચય મેટ્રિક્સની જરૂર અને ઉકેલની ગુણવત્તાના મૂલ્યાંકનમાં આંતરિક મુશ્કેલીઓ વિશે જાગૃતિ જરૂરી છે. આ પદ્ધતિનો યોગ્ય ઉપયોગ કરવા માટે મેટ્રિક્સની સ્થિતિ અને સંખ્યાત્મક સ્થિરતાના પાસાઓને ધ્યાનમાં લેવા આવશ્યક છે.