પુનરાવર્તક પદ્ધતિઓ દ્વારા ફંક્શનના મૂળ શોધવા - મૌખિક પરીક્ષાની તૈયારી

પરિચય

આ રિપોર્ટ ગાણિતિક ફંક્શન f : [a, b] → R ના વાસ્તવિક મૂળો શોધવા માટે પુનરાવર્તક પદ્ધતિઓ (iterative methods) વિશે વિસ્તૃત માહિતી પ્રદાન કરે છે. આ પદ્ધતિઓ સંખ્યાત્મક વિશ્લેષણ (numerical analysis) માં અત્યંત મહત્વપૂર્ણ છે અને વ્યવહારિક સમસ્યાઓ ઉકેલવા માટે વ્યાપકપણે ઉપયોગમાં લેવાય છે^1.

ન્યૂટન-રાફસન પદ્ધતિ - એક નક્કર ઉદાહરણ

મૂળભૂત સિદ્ધાંત

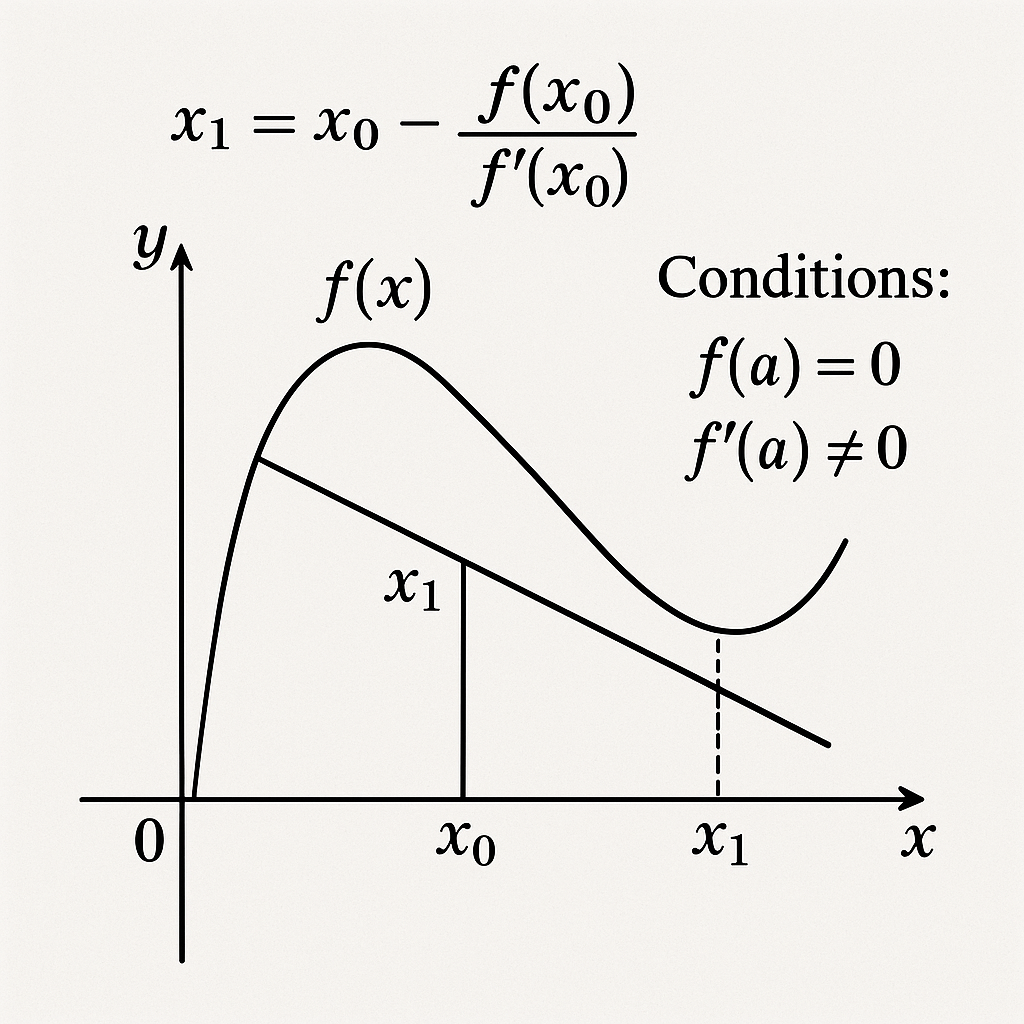
ન્યૂટન-રાફસન પદ્ધતિ સૌથી લોકપ્રિય અને શક્તિશાળી પુનરાવર્તક પદ્ધતિઓમાંની એક છે. આ પદ્ધતિ ટેન્જન્ટ લાઈનના સિદ્ધાંત પર આધારિત છે^2.

મૂળભૂત સૂત્ર:
$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

Newton-Raphson method formula and prerequisites diagram

નક્કર ઉદાહરણ: √2 શોધવું

ચાલો f(x) = x² - 2 ફંક્શનનું મૂળ શોધીએ, જે √2 આપશે.

આપેલ:

• f(x) = x² - 2
• f'(x) = 2x
• પ્રારંભિક મૂલ્ય: x₀ = 1.5

પુનરાવર્તક સૂત્ર:
$x_{n+1} = x_n - \frac{x_n^2 - 2}{2x_n}$

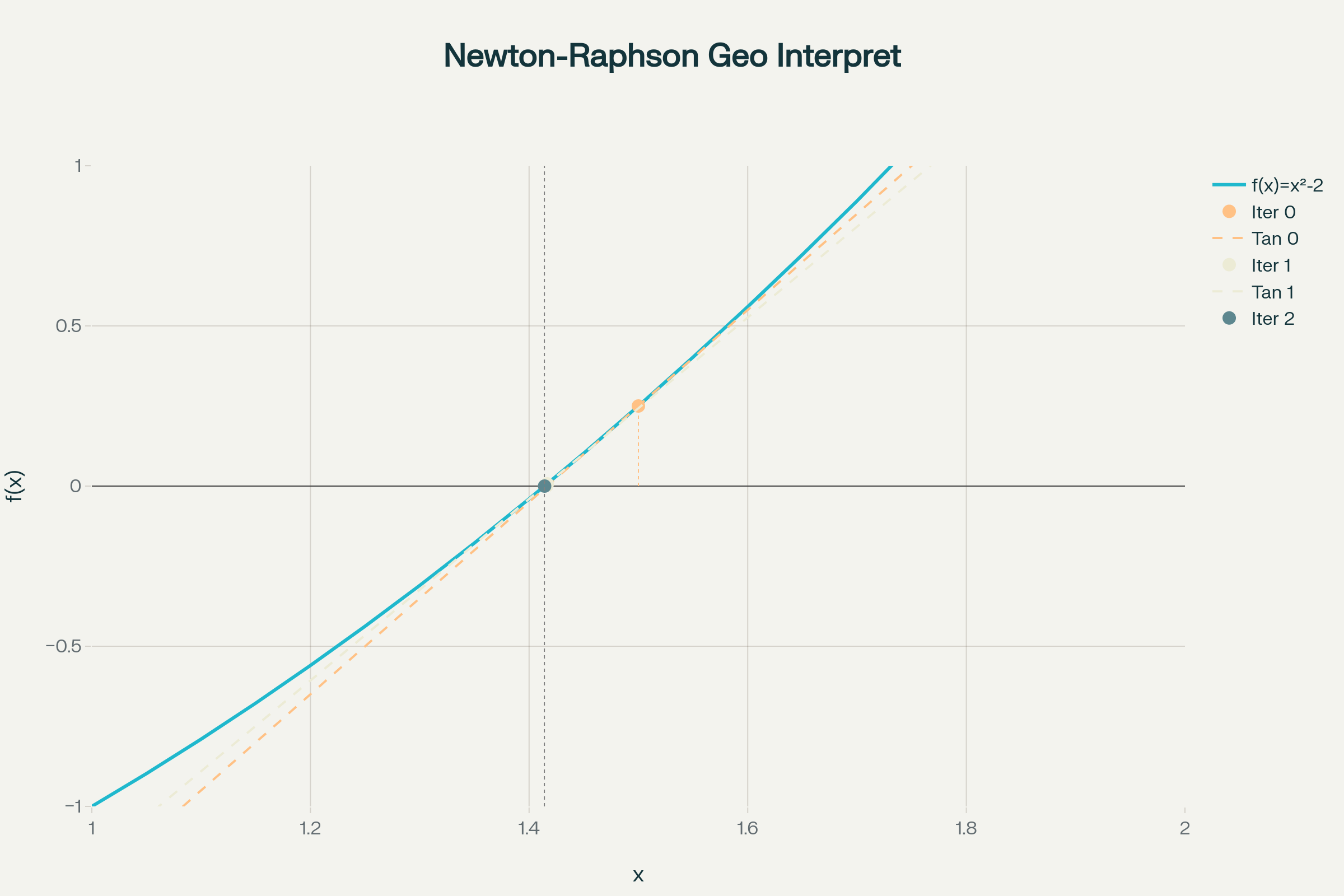
Geometric visualization of Newton-Raphson method showing how tangent lines lead to successive approximations

આ ઉદાહરણમાં આપણે જોઈ શકીએ છીએ કે માત્ર 4 પુનરાવર્તનમાં અસાધારણ ચોકસાઈ પ્રાપ્ત થાય છે.

પદ્ધતિ લાગુ કરવા માટેની પૂર્વશરતો

ન્યૂટન-રાફસન પદ્ધતિ માટે જરૂરી શરતો

1. વિકલન યોગ્યતા (Differentiability): ફંક્શન f(x) વિકલન યોગ્ય હોવું જોઈએ^2
2. અશૂન્ય વ્યુત્પન્ન (Non-zero Derivative): f'(x) ≠ 0 મૂળની નજીક હોવું જોઈએ^2
3. યોગ્ય પ્રારંભિક બિંદુ (Good Starting Point): x₀ મૂળની નજીક હોવું જોઈએ^2
4. સતત વ્યુત્પન્ન: વધુ ચોકસાઈ માટે f(x) ઓછામાં ઓછું ત્રણ વખત સતત વિકલન યોગ્ય હોવું જોઈએ^2

દ્વિભાજન પદ્ધતિ (Bisection Method) માટે જરૂરી શરતો

1. સતતતા (Continuity): f(x) અંતરાલ [a, b] પર સતત હોવું જોઈએ^1
2. મધ્યવર્તી મૂલ્ય પ્રમેય (Intermediate Value Theorem): f(a) · f(b) < 0^1

કન્વર્જન્સ ઓર્ડર (Convergence Order)

વ્યાખ્યા

કન્વર્જન્સ ઓર્ડર એ માપદંડ છે જે દર્શાવે છે કે પુનરાવર્તક પદ્ધતિ કેટલી ઝડપથી મૂળ સુધી પહોંચે છે^2.

ગાણિતિક વ્યાખ્યા:
$|x_{n+1} - r| \leq C|x_n - r|^p$

જ્યાં:

• r = સાચું મૂળ
• C = સ્થિર (constant)
• p = કન્વર્જન્સ ઓર્ડર

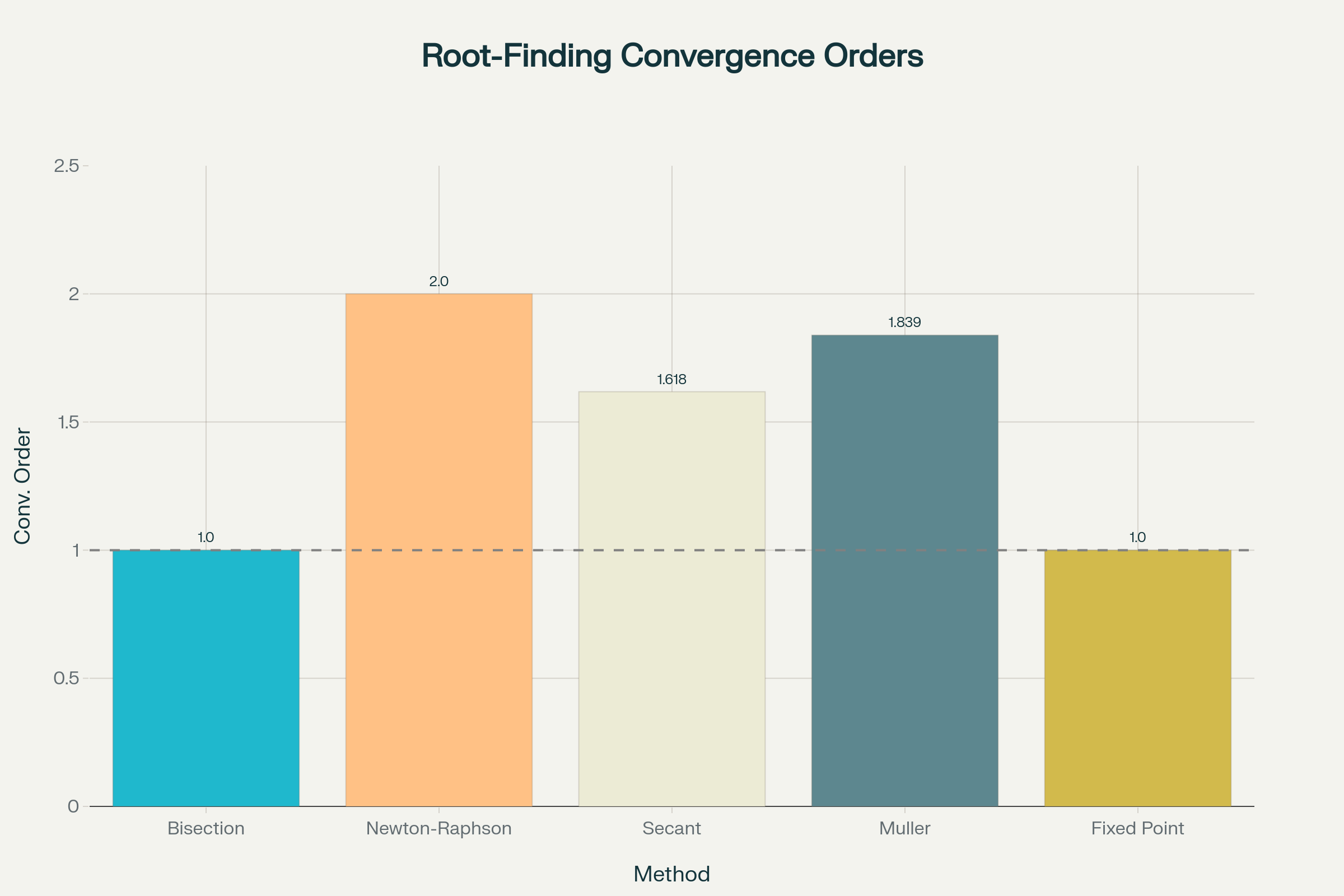
Bar chart showing convergence orders of different iterative root-finding methods

વિવિધ પદ્ધતિઓના કન્વર્જન્સ ઓર્ડર

મુખ્ય કન્વર્જન્સ પ્રકારો:

1. રેખીય કન્વર્જન્સ (p = 1): દ્વિભાજન પદ્ધતિ, સ્થિર બિંદુ પુનરાવર્તન
2. વર્ગાત્મક કન્વર્જન્સ (p = 2): ન્યૂટન-રાફસન પદ્ધતિ
3. અતિરેખીય કન્વર્જન્સ (1 < p < 2): સેકન્ટ પદ્ધતિ (p ≈ 1.618), મુલર પદ્ધતિ (p ≈ 1.839)

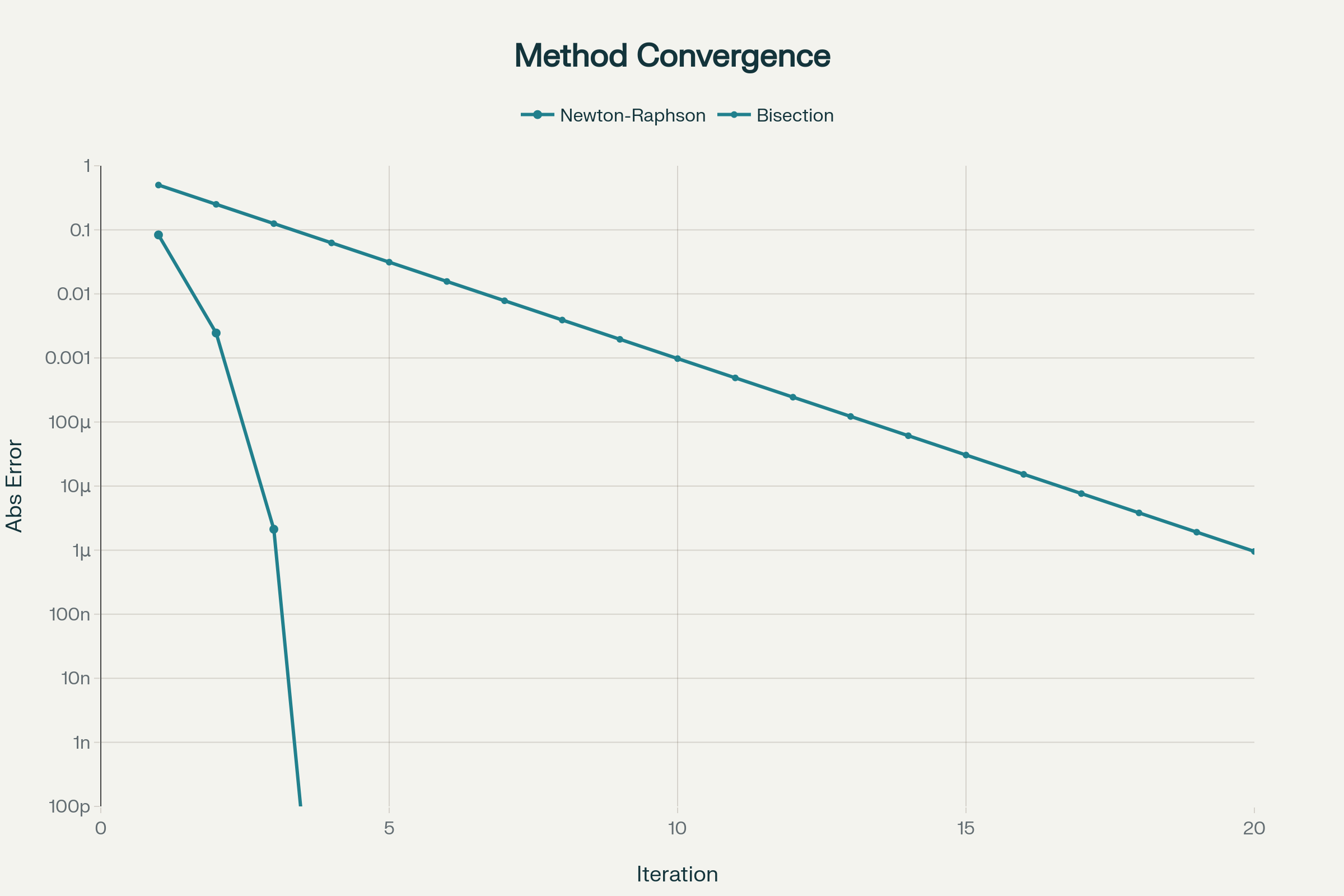
Convergence speed comparison showing Newton-Raphson's quadratic convergence vs Bisection's linear convergence

પોલિનોમિયલ ડિફ્લેશન (Polynomial Deflation)

સિદ્ધાંત

જ્યારે પોલિનોમિયલનું એક મૂળ જાણીતું હોય, ત્યારે આપણે વ્યવસ્થિત રીતે અન્ય મૂળો શોધી શકીએ છીએ. આ પ્રક્રિયાને પોલિનોમિયલ ડિફ્લેશન કહેવાય છે^1.

પદ્ધતિ

જો P(x) એક પોલિનોમિયલ છે અને r એ તેનું મૂળ છે, તો:
$P(x) = (x - r) \cdot Q(x)$

જ્યાં Q(x) એ ઘટાડેલું પોલિનોમિયલ છે.

મોડિફાઈડ ન્યૂટન-રાફસન સૂત્ર

જાણીતા મૂળો r₁, r₂, ..., rₖ માટે:
$x_{n+1} = x_n - \frac{P(x_n)}{P'(x_n)} \cdot \frac{1}{\prod_{i=1}^{k}(x_n - r_i)}$

પ્રાયોગિક ઉદાહરણ

P(x) = x³ - 6x² + 11x - 6 = (x-1)(x-2)(x-3) માટે:

1. પહેલું મૂળ: x₀ = 0.5 થી શરૂ કરીને r₁ = 1.0 મળે છે
2. બીજું મૂળ: r₁ નો ઉપયોગ કરીને x₀ = 1.5 થી r₂ = 2.0 મળે છે
3. ત્રીજું મૂળ: r₁ અને r₂ નો ઉપયોગ કરીને x₀ = 2.5 થી r₃ = 3.0 મળે છે

પદ્ધતિઓની તુલના

કાર્યક્ષમતા વિશ્લેષણ

ચોકસાઈ 10⁻¹⁰ માટે જરૂરી પુનરાવર્તનો:

• ન્યૂટન-રાફસન: 4 પુનરાવર્તનો
• દ્વિભાજન: 35 પુનરાવર્તનો

ફાયદા અને મર્યાદાઓ

ન્યૂટન-રાફસન પદ્ધતિ:

• ફાયદા: અત્યંત ઝડપી કન્વર્જન્સ (વર્ગાત્મક)
• મર્યાદાઓ: વ્યુત્પન્ન જરૂરી, કન્વર્જ નહીં થઈ શકે

દ્વિભાજન પદ્ધતિ:

• ફાયદા: હમેશા કન્વર્જ થાય છે, મજબૂત
• મર્યાદાઓ: ધીમી કન્વર્જન્સ (રેખીય)

નિષ્કર્ષ

પુનરાવર્તક પદ્ધતિઓ ગાણિતિક સમસ્યાઓ ઉકેલવા માટે શક્તિશાળી સાધનો છે. ન્યૂટન-રાફસન પદ્ધતિ તેની વર્ગાત્મક કન્વર્જન્સને કારણે ખાસ કરીને અસરકારક છે, જ્યારે દ્વિભાજન પદ્ધતિ તેની વિશ્વસનીયતા માટે મહત્વપૂર્ણ છે. પોલિનોમિયલ ડિફ્લેશન ટેકનિક બહુવિધ મૂળોવાળી સમસ્યાઓ માટે વ્યવસ્થિત ઉકેલ પ્રદાન કરે છે.

મૌખિક પરીક્ષા માટે આ મુખ્ય બાબતોને યાદ રાખો: પૂર્વશરતો, કન્વર્જન્સ ઓર્ડર, અને પ્રાયોગિક અમલીકરણની વિગતો^3.