પ્રાકૃતિક સંખ્યાઓ સાથે અંકગણિત અલ્ગોરિધમ્સ: શાળા પદ્ધતિ અને કરાત્સુબા પદ્ધતિ

આ રિપોર્ટ મૌખિક ગણિત પરીક્ષાની તૈયારી માટે પ્રાકૃતિક સંખ્યાઓના ગુણાકાર અને સરવાળાની પરંપરાગત અને આધુનિક પદ્ધતિઓનું વિશ્લેષણ પ્રસ્તુત કરે છે^1.

શાળા પદ્ધતિથી સરવાળો (Addition)

પદ્ધતિની પ્રક્રિયા

શાળામાં શીખવવામાં આવતી સરવાળાની પદ્ધતિ બિટ-બાય-બિટ આધારિત છે. બે પ્રાકૃતિક સંખ્યાઓ z₁ અને z₂ નો સરવાળો કરવા માટે અમે જમણેથી ડાબે તરફ દરેક અંકને કેરી સાથે ઉમેરીએ છીએ^1.

ઉદાહરણ - દ્વિસંકેતિક સંખ્યાઓ સાથે

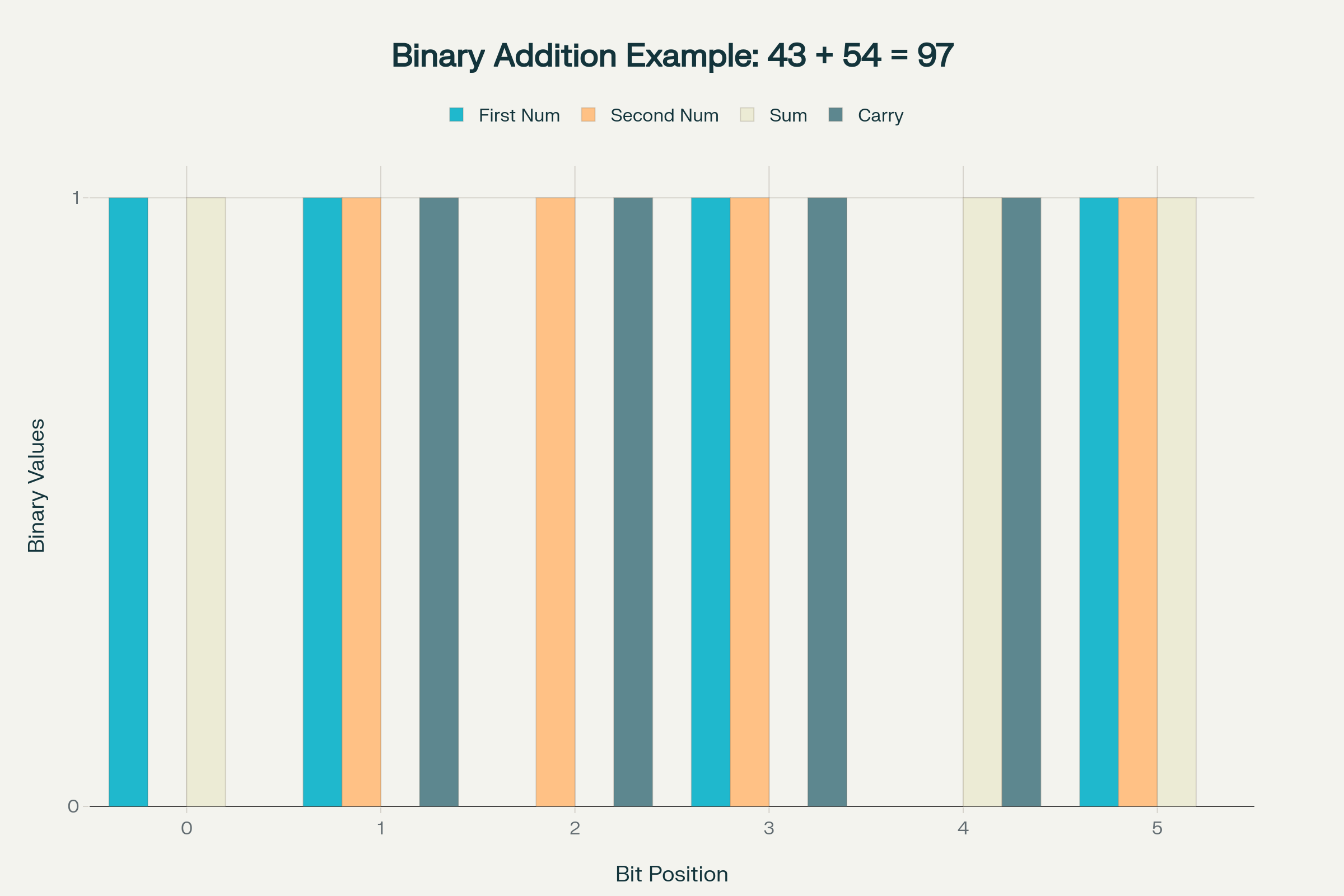
બે 6-બિટ દ્વિસંકેતિક સંખ્યાઓનું ઉદાહરણ લેવાય:

• z₁ = (1,0,1,0,1,1) = 43₁₀
• z₂ = (1,1,0,1,1,0) = 54₁₀

Step-by-step binary addition process showing how carries propagate through bit positions

દરેક સ્થાન પર કેરીનો પ્રસાર થાય છે:

• સ્થાન 0: 1 + 0 = 1 (કેરી = 0)
• સ્થાન 1: 1 + 1 = 0 (કેરી = 1)
• સ્થાન 2: 0 + 1 + 1 = 0 (કેરી = 1)
• અને આમ આગળ...

પરિણામ: (1,1,0,0,0,0,1) = 97₁₀^1

સમય જટિલતા

શાળા પદ્ધતિથી સરવાળો કરવા માટે O(n) સમય લાગે છે, જ્યાં n એ બિટ્સની સંખ્યા છે. આ શ્રેષ્ઠ શક્ય સમય જટિલતા છે કારણ કે દરેક બિટને ઓછામાં ઓછું એક વખત જોવું આવશ્યક છે^1.

શાળા પદ્ધતિથી ગુણાકાર (Multiplication)

પદ્ધતિની પ્રક્રિયા

પરંપરાગત ગુણાકાર પદ્ધતિમાં અમે દ્વિતીય સંખ્યાના દરેક અંક માટે આંશિક ગુણાકાર બનાવીએ છીએ અને તે બધાને ઉમેરીએ છીએ^1.

ઉદાહરણ - દ્વિસંકેતિક ગુણાકાર

z₁ = (1,0,1,0,1,1) અને z₂ = (1,1,0,1,1,0) માટે:

1. z₂ ના દરેક '1' બિટ માટે આંશિક ગુણાકાર બનાવો:
   • h₁ = (0,0,0,0,1,0,1,0,1,1,0)
   • h₂ = (0,0,0,1,0,1,0,1,1,0,0)
   • h₄ = (0,1,0,1,0,1,1,0,0,0,0)
   • h₅ = (1,0,1,0,1,1,0,0,0,0,0)
2. બધા આંશિક ગુણાકારોને ઉમેરો
   પરિણામ: (1,0,0,1,0,0,0,1,0,0,1,0) = 2322₁₀^1

સમય જટિલતા

શાળા પદ્ધતિથી ગુણાકાર કરવા માટે O(n²) સમય લાગે છે. આ બહુ બિટ્સવાળી મોટી સંખ્યાઓ માટે કાર્યક્ષમ નથી અને નોંધપાત્ર રીતે ઘટાડી શકાય છે^1.

કરાત્સુબા અલ્ગોરિધમ - મૂળભૂત વિચાર

સુધારણાનો મૂળ વિચાર

કરાત્સુબા અલ્ગોરિધમનો મૂળ વિચાર ડિવાઇડ એન્ડ કોન્કર અભિગમ પર આધારિત છે. બે n-બિટ સંખ્યાઓના ગુણાકાર માટે શાળા પદ્ધતિમાં 4 આંશિક ગુણાકાર જરૂરી છે, પરંતુ કરાત્સુબા માત્ર 3 આંશિક ગુણાકાર વાપરે છે^1.

અલ્ગોરિધમના પગલાં

n ≥ 5 બિટ્સવાળી સંખ્યાઓ માટે:

1. વિભાજન: k = ⌊n/2⌋ નક્કી કરો
2. ભાગો બનાવો:
   • a' = ઉચ્ચ k બિટ્સ, a = નીચ k બિટ્સ
   • b' = ઉચ્ચ k બિટ્સ, b = નીચ k બિટ્સ
3. સરવાળો: A = a' + a, B = b' + b
4. ત્રણ પુનરાવર્તક કૉલ્સ:
   • P₁ = a' × b'
   • P₂ = A × B
   • P₃ = a × b
5. પરિણામ: z = P₁ × 2²ᵏ + (P₂ - P₁ - P₃) × 2ᵏ + P₃^1

કરાત્સુબા રિકર્શન વૃક્ષ

વૃક્ષ માળખું

કરાત્સુબા અલ્ગોરિધમ રિકર્શન વૃક્ષ બનાવે છે જ્યાં:

• દરેક સ્તરે 3 ગણા વધુ નોડ્સ હોય છે
• દરેક નોડ અડધા કદની સમસ્યા સાથે કામ કરે છે
• n ≤ 4 સુધી વૃક્ષ વધે છે (બેઝ કેસ)^1

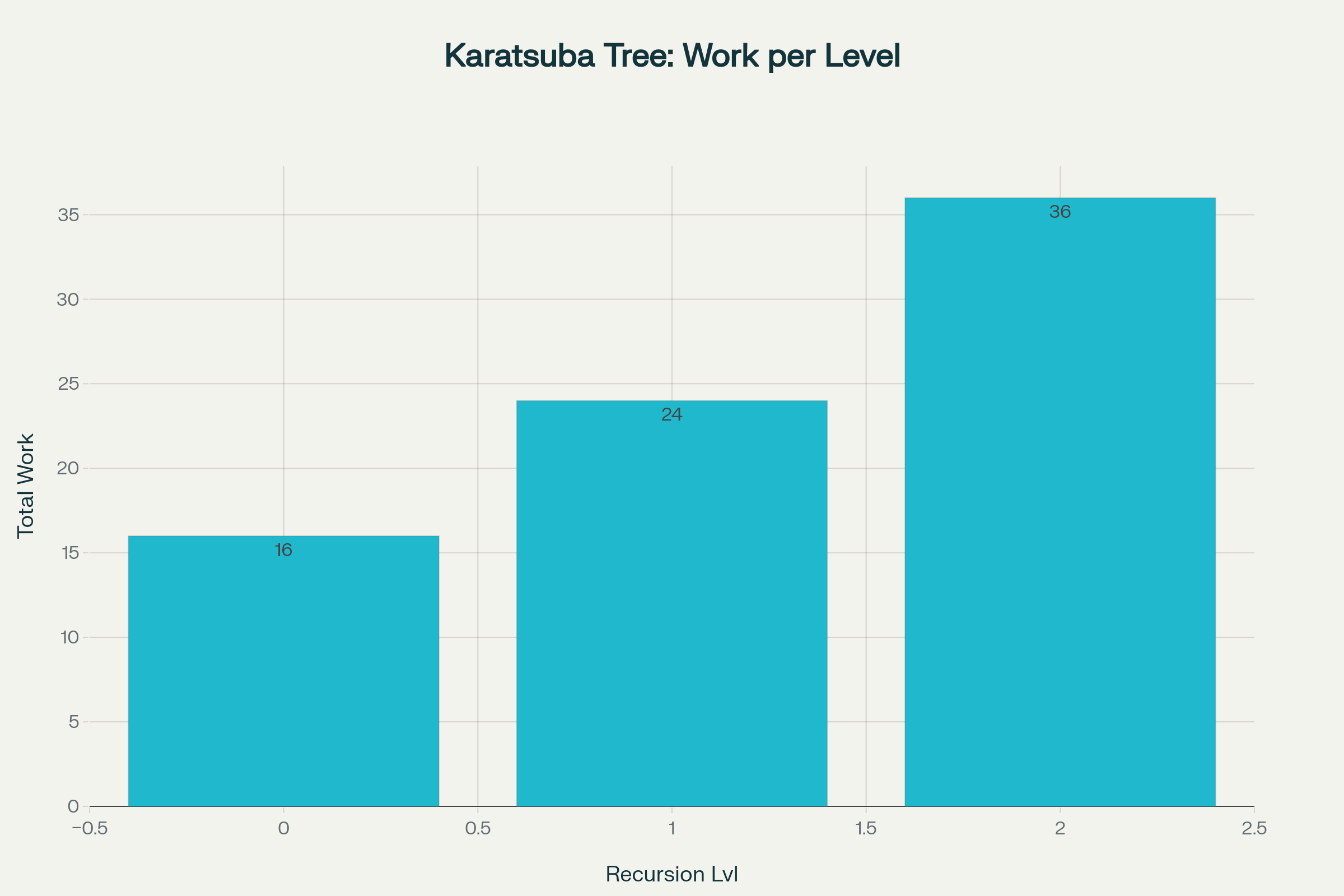
Work distribution across recursion levels in Karatsuba algorithm showing increasing work per level

સમય જટિલતા ગણતરી

દરેક સ્તર i માટે:

• નોડ્સની સંખ્યા: 3ⁱ
• કાર્ય પ્રતિ સ્તર: 3ⁱ × (n/2ⁱ) = 3ⁱ × n/2ⁱ

કુલ સ્તરો: d = ⌊log₂(n/2)⌋

કુલ સમય જટિલતા:
T(n) = Σᵢ₌₀ᵈ (3/2)ⁱ × n = n × (3/2)ᵈ⁺¹-1 / (3/2-1) = O(n^log₂(3)) = O(n^1.58)^1

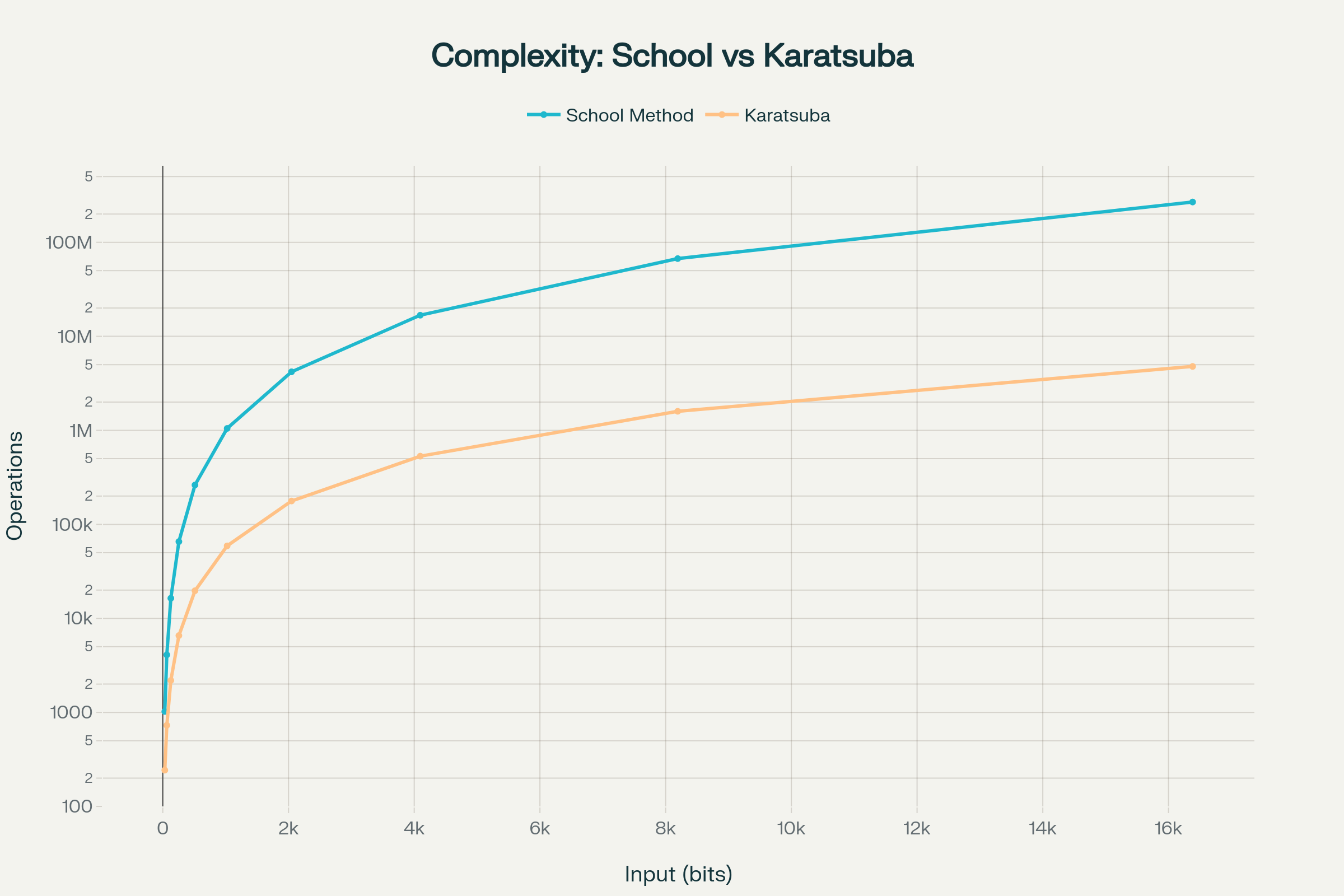
Comparison of time complexity between the school multiplication method and Karatsuba algorithm showing significant improvement for larger inputs

કરાત્સુબા ક્યારે ધીમું છે?

નાની સંખ્યાઓ માટે

કરાત્સુબા અલ્ગોરિધમ નાની સંખ્યાઓ (n ≤ 4-8 બિટ્સ) માટે શાળા પદ્ધતિ કરતાં ધીમું છે કારણ કે:

1. ઓવરહેડ: રિકર્શન કૉલ્સ અને વધારાના ગણતરીઓ
2. કોન્સ્ટન્ટ ફેક્ટર: શાળા પદ્ધતિ સરળ અને સીધી છે
3. મેમરી ઍક્સેસ: વધારાના વેરિએબલ્સ અને સ્ટેક સ્પેસ^1

પ્રેક્ટિકલ કંસિડરેશન

વાસ્તવિક અમલીકરણમાં સામાન્યતે હાઇબ્રિડ અભિગમ વાપરવામાં આવે છે:

• નાની સંખ્યાઓ માટે શાળા પદ્ધતિ
• મોટી સંખ્યાઓ (સામાન્યતે > 1000 બિટ્સ) માટે કરાત્સુબા^1

નિષ્કર્ષ

કરાત્સુબા અલ્ગોરિધમ મોટી સંખ્યાઓના ગુણાકાર માટે નોંધપાત્ર સુધારણા લાવે છે, O(n²) ને O(n^1.58) માં ઘટાડીને. તેની રિકર્શન વૃક્ષ વિશ્લેષણ દ્વારા અમે સમજી શકીએ છીએ કે કેવી રીતે ડિવાઇડ એન્ડ કોન્કર તકનીક વધુ કાર્યક્ષમ અલ્ગોરિધમ્સ બનાવવામાં મદદ કરે છે. આજકાલ RSA ક્રિપ્ટોગ્રાફી અને અન્ય એપ્લિકેશન્સમાં હજારો બિટ્સવાળી મોટી સંખ્યાઓ માટે આવી પદ્ધતિઓ અત્યંત જરૂરી છે^1.