નેટવર્કમાં મહત્તમ પ્રવાહ (Maximum Flow) - વિગતવાર અભ્યાસ
નેટવર્કમાં મહત્તમ પ્રવાહની ગણતરી એ કોમ્પ્યુટર સાયન્સ અને ઓપરેશન્સ રિસર્ચનો એક મહત્વપૂર્ણ વિષય છે. આ સમસ્યા વિવિધ વાસ્તવિક જીવનની પરિસ્થિતિઓમાં જોવા મળે છે, જેમ કે ટ્રાફિક નેટવર્ક, સપ્લાય ચેઇન, અને ડેટા ટ્રાન્સમિશન સિસ્ટમ્સ.
મહત્તમ પ્રવાહ સમસ્યા માટે નીચેના ઘટકો આવશ્યક છે^1:
- નિર્દેશિત ગ્રાફ G(V, E): જ્યાં V એ vertices (નોડ્સ) અને E એ edges (કિનારીઓ) છે
- સ્ત્રોત (Source) s: જ્યાંથી પ્રવાહ શરૂ થાય છે
- લક્ષ્ય (Sink) t: જ્યાં પ્રવાહ સમાપ્ત થાય છે
- ક્ષમતા (Capacity) ce: દરેક edge e માટે એક વાસ્તવિક સંખ્યા જે તે edge દ્વારા વહી શકે તેવા મહત્તમ પ્રવાહને દર્શાવે છે
- શરત: બધી ક્ષમતાઓ પ્રાકૃતિક સંખ્યાઓ છે અને ≥ 1 છે
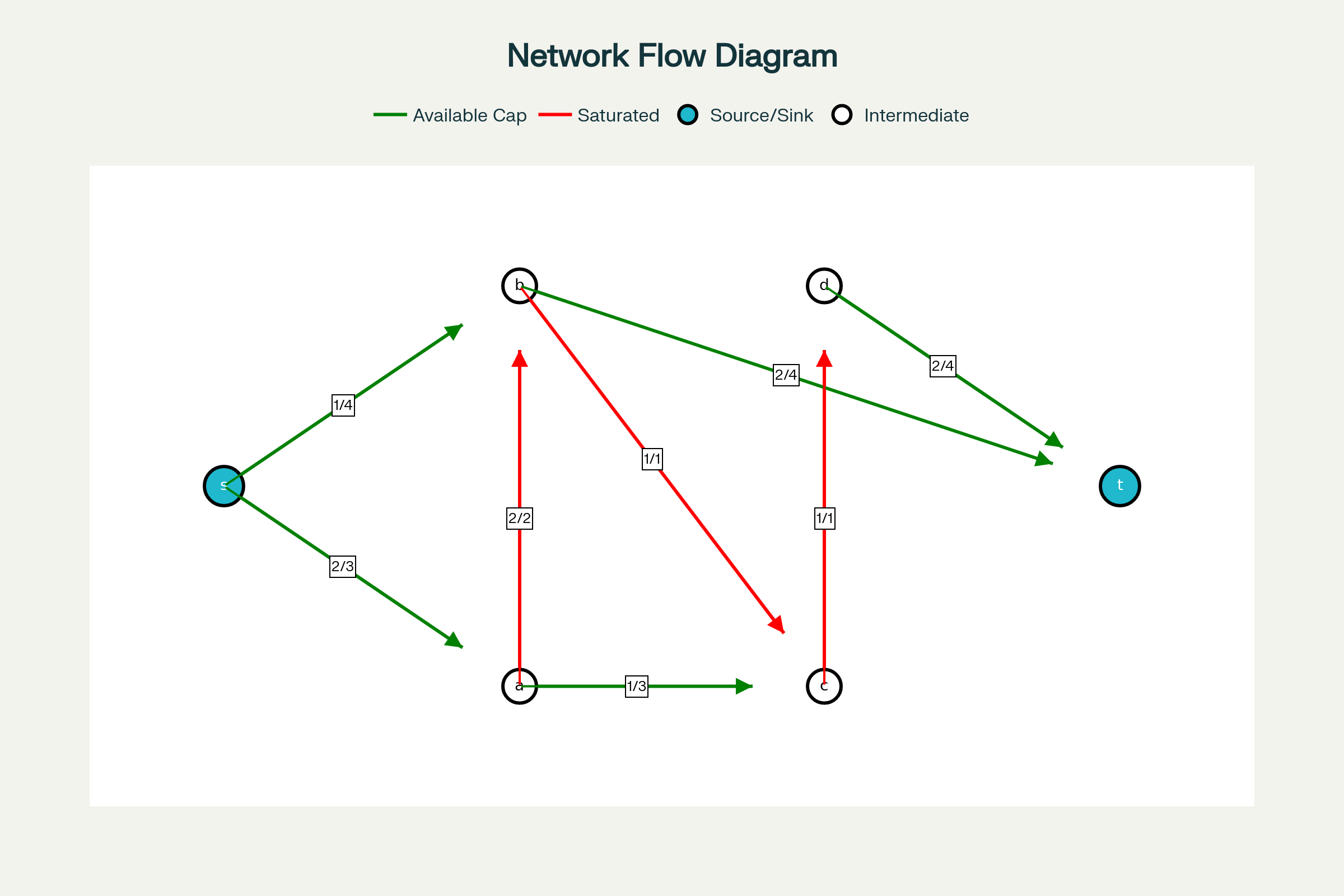
Network Flow Example: Current flow (2/3 means flow=2, capacity=3)
આઉટપુટ (Output)
- મહત્તમ પ્રવાહ f: સ્ત્રોત sથી લક્ષ્ય t સુધીનો મહત્તમ પ્રવાહ મૂલ્ય
- પ્રવાહ ફંક્શન: દરેક edge e માટે fe જે 0 ≤ fe ≤ ce સંતોષે છે
- સંરક્ષણ સિદ્ધાંત: s અને t સિવાયના બધા નોડ્સ માટે, આવનાર પ્રવાહ = જનાર પ્રવાહ
વ્યવહારિક ઉપયોગનું ઉદાહરણ
Job Scheduling અને Processor Allocation
એક મહત્વપૂર્ણ ઉપયોગ છે કામ (Jobs) નું પ્રોસેસર પર વિતરણ^1:
- સ્થિતિ: k કામો (J₁, J₂, ..., Jₖ) અને ℓ પ્રોસેસર્સ (P₁, P₂, ..., Pₗ)
- અવરોધો:
- દરેક કામ Jᵢ નો execution time hᵢ છે
- દરેક પ્રોસેસર Pⱼ ની મફત ક્ષમતા cⱼ છે
- કોઈ કામ કોના પ્રોસેસર પર ચાલી શકે તેની મર્યાદાઓ છે
નેટવર્ક મોડેલ:
- સ્ત્રોત s થી દરેક કામ સુધી hᵢ ક્ષમતાની edge
- કામોથી પ્રોસેસર્સ સુધી અમર્યાદિત ક્ષમતાની edges (જ્યાં માન્ય હોય)
- દરેક પ્રોસેસરથી લક્ષ્ય t સુધી cⱼ ક્ષમતાની edge
સવર્ધક માર્ગ (Augmenting Path) નો ખ્યાલ
વ્યાખ્યા
સવર્ધક માર્ગ એ સ્ત્રોત s થી લક્ષ્ય t સુધીનો એવો માર્ગ છે જ્યાં આપણે હજુ પણ વધારાનો પ્રવાહ મોકલી શકીએ છીએ^1.
સવર્ધક માર્ગની શરતો:
- આગળની દિશામાં: જો edge (u,v) આગળની દિશામાં છે, તો fe < ce (હજુ ક્ષમતા બાકી છે)
- પાછળની દિશામાં: જો edge (u,v) પાછળની દિશામાં છે, તો fe > 0 (પ્રવાહ ઘટાડી શકાય)
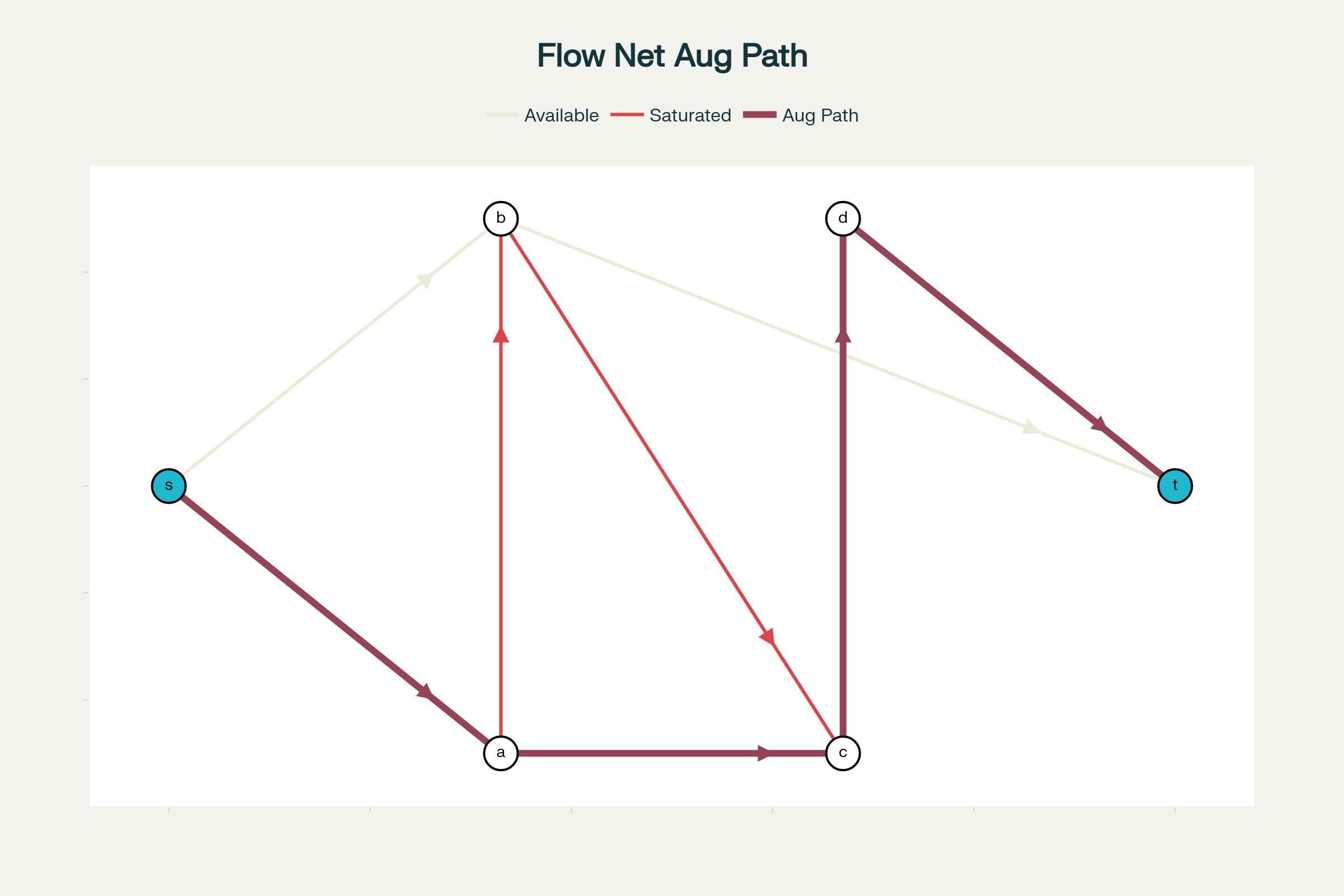
Augmenting Path Example: Path s→a→c→d→t with bottleneck capacity 1
ઉદાહરણ
ઉપરના ચિત્રમાં, માર્ગ s→a→c→d→t એક સવર્ધક માર્ગ છે કારણ કે:
- s→a: 2/3 (1 વધુ એકમ મોકલી શકાય)
- a→c: 1/3 (2 વધુ એકમ મોકલી શકાય)
- c→d: 1/1 (saturated, પણ backward direction માં ઘટાડી શકાય)
- d→t: 2/4 (2 વધુ એકમ મોકલી શકાય)
મુક્ત ક્ષમતા (Free Capacity): આ માર્ગની ન્યૂનતમ ઉપલબ્ધ ક્ષમતા = min(1, 2, 1, 2) = 1
સવર્ધક માર્ગની અસ્તિત્વ તપાસવી
Algorithm (BFS આધારિત)
સવર્ધક માર્ગની અસ્તિત્વ તપાસવા માટે નીચેનું algorithm વાપરાય છે^1:
- પ્રારંભિકીકરણ:
- R = {s} (પહોંચેલા નોડ્સ)
- S = ∅ (પ્રોસેસ થયેલા નોડ્સ)
- પુનરાવર્તન: જ્યાં સુધી R ≠ S
- v ∈ R - S પસંદ કરો
- દરેક આગળની edge (v,w) માટે જ્યાં fe < ce, w ને R માં ઉમેરો
- દરેક પાછળની edge (w,v) માટે જ્યાં fe > 0, w ને R માં ઉમેરો
- v ને S માં ઉમેરો
- પરીક્ષણ: જો t ∈ R, તો સવર્ધક માર્ગ અસ્તિત્વમાં છે
Ford-Fulkerson પદ્ધતિ
મૂળભૂત Algorithm
Ford-Fulkerson પદ્ધતિ વ્યવસ્થિત રીતે મહત્તમ પ્રવાહ શોધે છે^1:
- પ્રારંભિકીકરણ: બધા edges માટે fe = 0
- પુનરાવર્તન: જ્યાં સુધી સવર્ધક માર્ગ મળે
- સવર્ધક માર્ગ શોધો
- તેની મુક્ત ક્ષમતા δ ગણો
- માર્ગ પર પ્રવાહ δ વધારો
- સમાપ્તિ: જ્યારે કોઈ સવર્ધક માર્ગ ન મળે
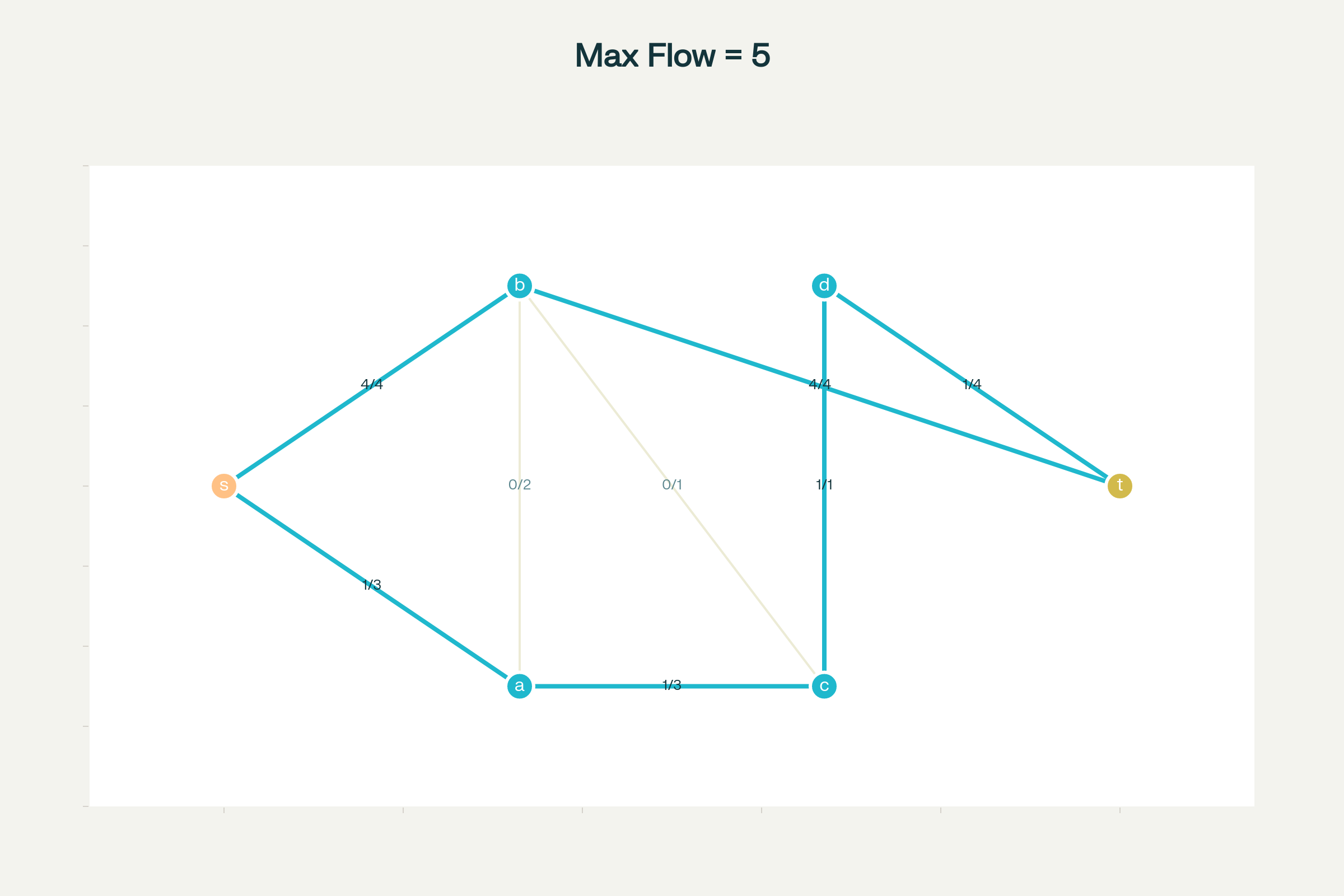
Ford-Fulkerson Algorithm Steps: Progressive increase of flow until maximum is reached
ચરણ-દર-ચરણ ઉદાહરણ:
ચરણ 1: શરૂઆતમાં બધે શૂન્ય પ્રવાહ
ચરણ 2: s→b→t માર્ગ મળ્યો, 4 એકમ પ્રવાહ વધાર્યો
ચરણ 3: s→a→c→d→t માર્ગ મળ્યો, 1 એકમ પ્રવાહ વધાર્યો
ચરણ 4: કોઈ વધુ સવર્ધક માર્ગ નથી, મહત્તમ પ્રવાહ = 5
સમય જટિલતા (Time Complexity)
મુખ્ય પરિણામો
Ford-Fulkerson પદ્ધતિની સમય જટિલતા નીચે પ્રમાણે છે^1:
| પદ્ધતિ |
સમય જટિલતા |
વર્ણન |
| મૂળભૂત Ford-Fulkerson |
O(max_flow_value) |
દરેક પુનરાવર્તનમાં ઓછામાં ઓછો 1 એકમ વધારો |
| Edmonds-Karp |
O(VE²) |
BFS વાપરીને સૌથી ટૂંકો સવર્ધક માર્ગ શોધે |
| સામાન્ય હદ |
O(VE × max_flow_value) |
V = નોડ્સ, E = edges |
મહત્વપૂર્ણ લક્ષણો:
- પૂર્ણતાની ખાતરી: Ford-Fulkerson હંમેશા સમાપ્ત થાય છે અને મહત્તમ પ્રવાહ શોધે છે
- પૂર્ણાંક પ્રવાહ: જો બધી ક્ષમતાઓ પૂર્ણાંક છે, તો મહત્તમ પ્રવાહ પણ પૂર્ણાંક હશે
- Max-Flow Min-Cut Theorem: મહત્તમ પ્રવાહ = ન્યૂનતમ cut ની ક્ષમતા
મૂળભૂત સિદ્ધાંત
મહત્વપૂર્ણ મેર્કે (Fundamental Principle)
મેર્કે 9.1: પ્રવાહ f મહત્તમ છે જો અને માત્ર જો કોઈ સવર્ધક માર્ગ અસ્તિત્વમાં નથી^1.
આ સિદ્ધાંત Ford-Fulkerson algorithm નો આધાર છે અને સુનિશ્ચિત કરે છે કે અમારી પદ્ધતિ સાચું પરિણામ આપે છે.
વ્યવહારિક મહત્વ
મહત્તમ પ્રવાહ algorithm નો ઉપયોગ આજે વિવિધ ક્ષેત્રોમાં થાય છે:
- ટ્રાફિક મેનેજમેન્ટ: શહેરમાં વાહન પ્રવાહ ઓપ્ટિમાઇઝ કરવા
- કોમ્પ્યુટર નેટવર્ક: ડેટા ટ્રાન્સમિશન ઓપ્ટિમાઇઝ કરવા
- સપ્લાય ચેઇન: માલસામાનનું વિતરણ ઓપ્ટિમાઇઝ કરવા
- ઇમેજ પ્રોસેસિંગ: ઇમેજ સેગમેન્ટેશન માટે
આ algorithm એ કોમ્પ્યુટર સાયન્સના સૌથી મહત્વપૂર્ણ અને ઉપયોગી algorithms પૈકી એક છે.
⁂



